
Gravitational hair for extreme Kerr black holes using a GPU-accelerated mixed-precision WENO method
A breakthrough discovery was made that a special kind of black hole violates black hole uniqueness, the so-called “no hair” theorem. Specifically, a computational study of extremal black holes — holes that are “saturated” with the maximum charge or spin they can possibly carry — found that there is a quantity that can be constructed from the spacetime curvature at the black hole horizon that is...


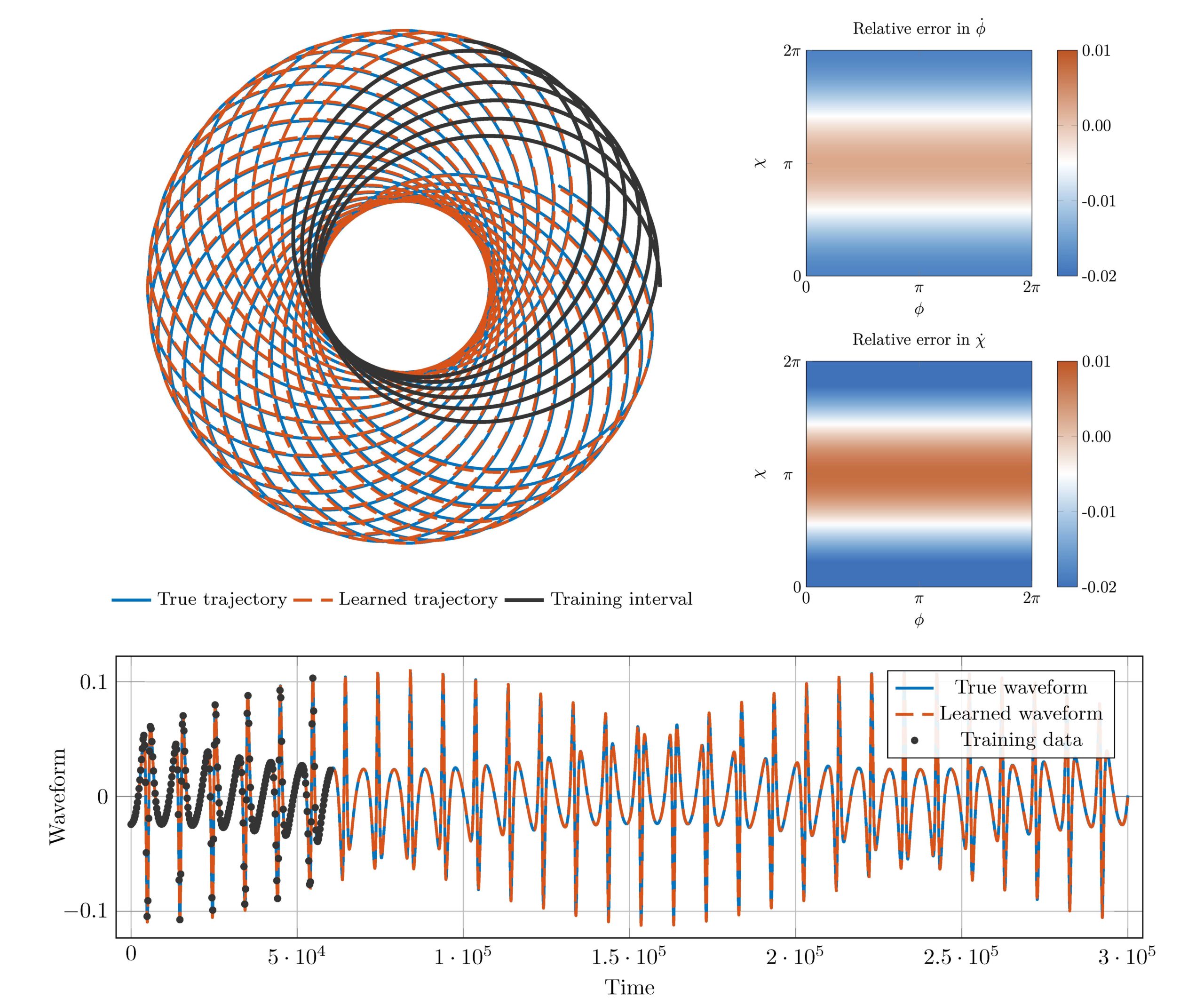
Orbital dynamics of binary black hole systems can be learned from gravitational wave measurements
The collision of massive compact objects, such as black holes (BHs) or neutron stars, emit an immense amount of energy in the form of gravitational waves. With the advent of advanced gravitational-wave detectors, such as the NSF-funded Laser Interferometer Gravitational-Wave Observatory (LIGO), we are now able to directly observe gravitational waves. Encoded in these waves are information about...

Summer School on Data, Dynamics, and COVID-19
How did the Covid pandemic affect carbon emissions in 2020? Does having a certain blood type make one more susceptible to Covid? What is the role of the uninsured population in driving the pandemic? These and many other questions were the focus of over forty graduate students and advanced undergraduates who participated in the 2020 AIM Online Summer School on Dynamics, Data and the COVID-19...


A Deep-learning Solution for the Schrödinger Equation
Solving the electronic Schrödinger equation is at the heart of computing and understanding in detail the physical and chemical properties of molecules and materials. They are of paramount importance for developing new drug molecules, biofuels or nanomaterials. Unfortunately the Schrödinger equation can only be solved exactly for the hydrogen atom, and the cost of highly accurate approximations...

Better Understanding of Betti Numbers
A simplicial complex is a set formed from points, line segments, triangles, and their higher-dimensional analogs. Betti numbers classify topological spaces according to the connectivity of simplicial complexes. The kth Betti number is the rank of the kth homology group and is the maximum number of cuts that can be made before separating a surface into two pieces. For some value n, Betti numbers...

Mathematicians solve one of the mysteries of two-dimensional shapes
Pure mathematicians like Daniel Cristofaro-Gardiner thrive on the creative challenge of imagining connections between things that seem unconnected and then using these connections to puzzle out old problems. Take the simplicity conjecture, which Cristofaro-Gardiner solved earlier this year with two of his colleagues. The conjecture emerged from the work of mathematicians who, during the...

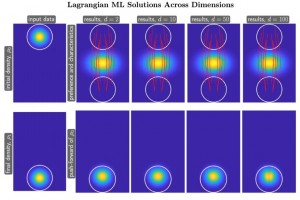
New Machine Learning Approach for Mean-Field Games
Mean field games are critical classes of multi-agent models for efficient analysis of massive populations of interacting agents with numerous applications ranging from economics to crowd motion. Their numerical solutions typically suffer from the curse of dimensionality. Numerical methods for mean field games were usually grid based. This effectively limited them to two and three dimensions....

Quasisymmetries for Quasiparticles
For an ordinary chemical such as water, the phase diagram shows which state the chemical likes to be in at different temperatures and pressures. Water, for example, has one liquid phase and seventeen solid phases (one of which is the cubical form that you think of as “ice”). Now, mathematicians have identified a theoretically feasible substance with an even more complicated phase diagram than...

The Math of Irreversibility
A relatively new branch of mathematics, called higher category theory, seeks to address a common but perplexing phenomenon in math as well as other sciences. “We’re trying to build tools that allow us to capture irreversibility,” says Ezra Getzler of Northwestern University, one of 47 mathematicians who participated in the 2020 spring program on “Higher Categories and Categorification” at the...

Algebraic Computer Vision Advances the 3D Reconstruction of Curves and Surfaces from Multiple Views
Contributed by: Ricardo Fabbri Given a series of ordinary photographs of coffee mugs over a table, can you guess where the photographer was located at each shot? In other words, given m central projections of piecewise smooth curves and surfaces, what are the translations and rotations of the underlying camera? The diagram below illustrates a case with m = 3 where the goal is to recover two...
