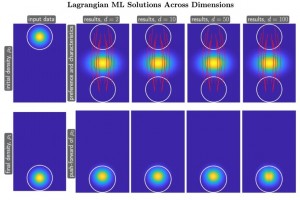
Mean field games are critical classes of multi-agent models for efficient analysis of massive populations of interacting agents with numerous applications ranging from economics to crowd motion. Their numerical solutions typically suffer from the curse of dimensionality. Numerical methods for mean field games were usually grid based. This effectively limited them to two and three dimensions. Within the 2020 IPAM spring program “High Dimensional Hamilton-Jacobi PDEs”, L. Ruthotto, S. Osher, W. Li, L. Nurbekyan and S. W. Fung developed a machine learning framework for solving these problems rapidly in as many as 100 dimensions. In contrast to the standard numerical methods, the complexity of this novel machine learning method in 100 dimensions is basically the same as that of a grid based method in two dimensions. This now allows the subject to advance to tackle realistic applications in a wide variety of fields.