Contributed by Olga Paris-Romaskevich

Tiling billiards is a mathematical model for the movement of light in heterogeneous media made from homogeneous pieces. Objects in water, seen through a flat surface, do appear magnified when the eye is close to the surface. Anyone who has used a diving mask is aware of it. The reason for this effect is the Snell’s law of refraction: light refracts when passing from one homogeneous media (air) to another (water), with different refraction indices. The ratio between these indices is called the refraction coefficient, for water and air it is close to 0.75. Tiling billiards model the propagation of light that travels through a tiling of the plane by polygons. One can imagine that neighboring tiles are made from homogeneous materials with different refraction indices. The case when the refraction coefficient is equal to -1 is of particular interest for the dynamics since it is related to the study of foliations on non-orientable surfaces with a flat metric. By now, only a few works exist on the subject. The simplest non-trivial case of a tiling billiard is a billiard on a periodic triangle tiling, introduced in [1] and subsequently studied in [2] and [3]. This tiling is given by three families of parallel equidistant lines on the plane, and defined, up to rescaling, by a fixed triangle on the plane. One of the trajectories of this tiling is shown on Figure 1.

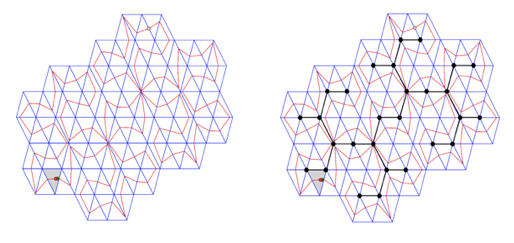
Figure 1: On the left, a periodic trajectory in a triangle tiling billiard.
On the right, a corresponding tree. A trajectory makes a tour of this tree.

It happens that all of the bounded trajectories in such a tiling are periodic. This fact may seem surprising since in a standard billiard theory, periodic trajectories are rare and hard to find. Indeed, it is still an open problem to find at least one periodic trajectory of a billiard in a triangle.

The reason for such a stability in the case of triangle tiling billiards, is the existence of a folding procedure, noticed in [1]. One can fold one tile on its neighbor in such a way that two parts of the trajectory fold into the same straight segment. Moreover, this construction can be done globally. In this case, all of the tiling maps inside a disk. By studying an induced map on its boundary (an interval exchange transformation on the circle), one manages to prove classification theorems for such billiards. In [2] some results were obtained and in [3] the symbolic dynamics was completely described.

One of the key results of [3] is the proof of the Tree Conjecture formulated in [1] concerning periodic trajectories of triangle tiling billiards. This Conjecture states the following: any periodic trajectory doesn’t contour any tile. In other words, a graph obtained as an intersection of the domain bounded by this trajectory and the initial lattice, is a tree, see Figure 1.

The results of [3] on tiling billiards show new connections of this system with many classical objects with, among others, the famous Rauzy gasket. A poster [4] with the results of [3] was presented at a poster session of Illustrating geometry and topology workshop of ICERM’s Illustrating mathematics program. Since then, a short animation movie was made by Ofir David, based on the results of [3]. No mathematical knowledge is needed to enjoy this movie but understanding mathematics will certainly help you enjoy it even more.

Figure 2: A snapshot from a movie made by Ofir David based on the research article [3].
Here, a cat jumps in a magic rain with tiling billiard properties.

References:

[1] P. Baird-Smith, D. Davis, E. Fromm, S. Iyer, Tiling billiards on triangle tilings, and interval exchange transformations , https://arxiv.org/abs/1809.07876 (2019)

[2] P. Hubert, O. Paris-Romaskevich Triangle tiling billiards and the exceptional family of their escaping trajectories: circumcenters and Rauzy gasket, Experimental mathematics (2019), https://www.tandfonline.com/doi/abs/10.1080/10586458.2019.1583615

[3] O. Paris-Romaskevich, Trees and flowers on a billiard table (2019+), submitted, https://hal.archives-ouvertes.fr/hal-02169195

[4] O. Paris-Romaskevich, poster Everything you wanted to know about triangle tiling billiards , for Illustrating mathematics, ICERM, Providence (2019), link: https://mathinstitutes.org/wp-content/uploads/2020/04/Illustrating-Math-Poster-1.pdf

[5] O. David, short animation movie Refraction tilings , on Dragonazible Youtube channel, https://www.youtube.com/watch?v=t1r1cO1V35I&t=34s