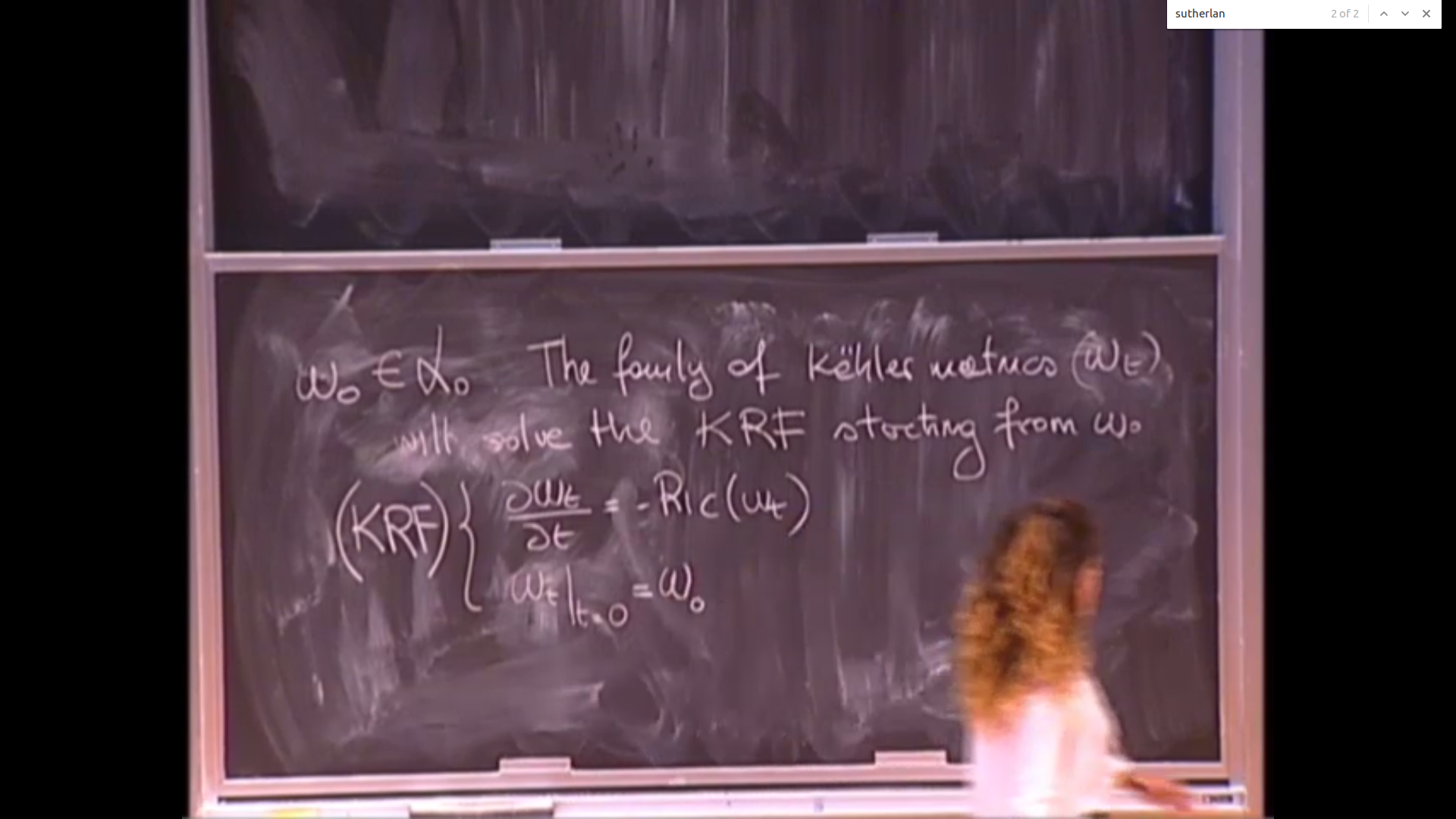Let X be a compact Kaehler manifold. I will show that the Kaehler-Ricci flow can be run from a degenerate initial data, (more precisely, from an arbitrary positive closed current) and that it is immediately smooth in a Zariski open subset of X. Moreover, if the initial data has positive Lelong number we indeed have propagation of singularities for short time. Finally, I will prove a uniqueness result in the case of zero Lelong numbers.