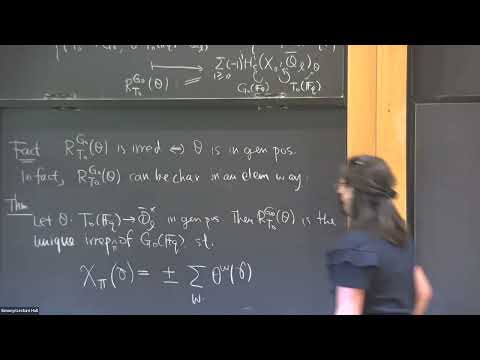Lusztig's theory of character sheaves for connected reductive groups is one of the most important developments in representation theory in the last few decades. In this talk, we will describe a construction which extends this "depth zero" picture to give positive-depth character sheaves associated to generic data. In the simplest nontrivial case, this resolves a conjecture of Lusztig and produces conjugation-equivariant simple perverse sheaves associated to sufficiently generic multiplicative local systems whose trace-of-Frobenius function coincides with parahoric Deligne--Lusztig induction. This is joint work with R. Bezrukavnikov.