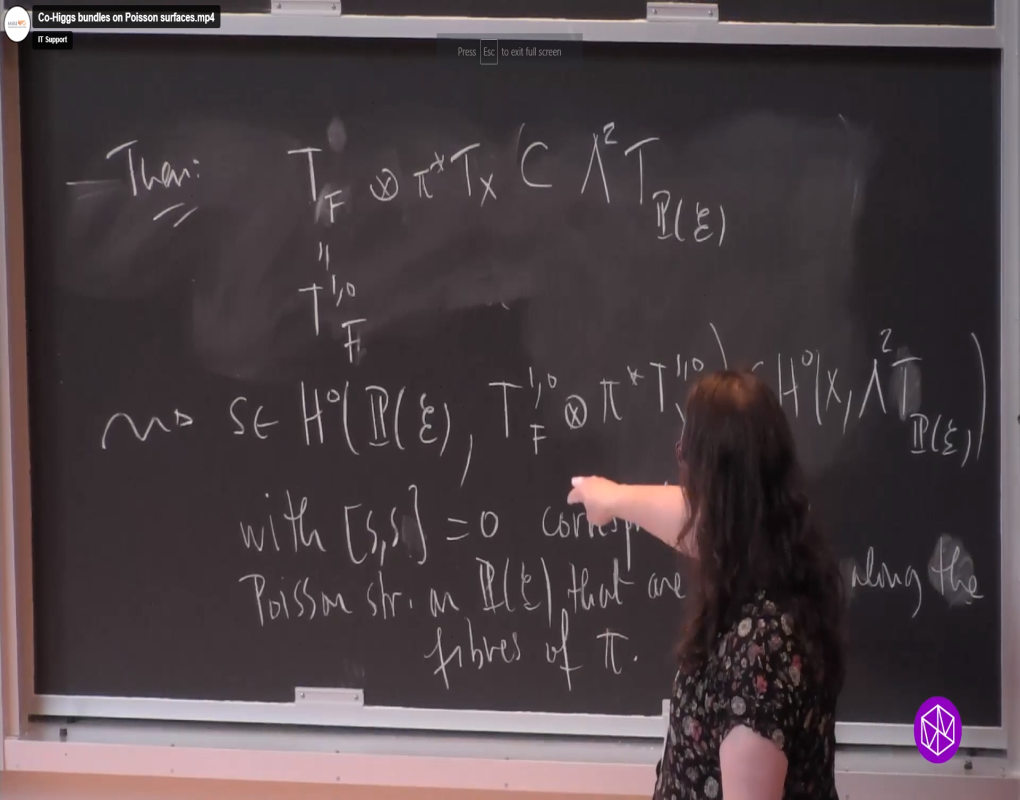Co-Higgs bundles on a complex manifold $M$ are given by pairs $(E,\phi)$ consisting of a holomorphic vector bundle $E$ on $M$ together with a Higgs field $\phi \in H^0(M,\rm{End}(E) \otimes TM)$ that satisfies certain integrability conditions. In particular, co-Higgs bundles correspond to generalized holomorphic bundles on complex manifolds. They also give rise to a special class of holomorphic Poisson structures on the projective bundles $\mathbb{P}(E)$. Co-Higgs bundles were first studied by S. Rayan on Riemann surfaces and $\mathbb{CP}^2$ in his thesis, where he also gave a non-existence theorem for stable, traceless rank-2 co-Higgs bundles on K3 and general-type surfaces. In this talk, we consider co-Higgs bundles on compact holomorphic Poisson surfaces. We give necessary and sufficient conditions for the existence of stable, traceless rank-2 co-Higgs bundles on all compact holomorphic Poisson surfaces as well as a complete classification of such bundles on some of these surfaces.