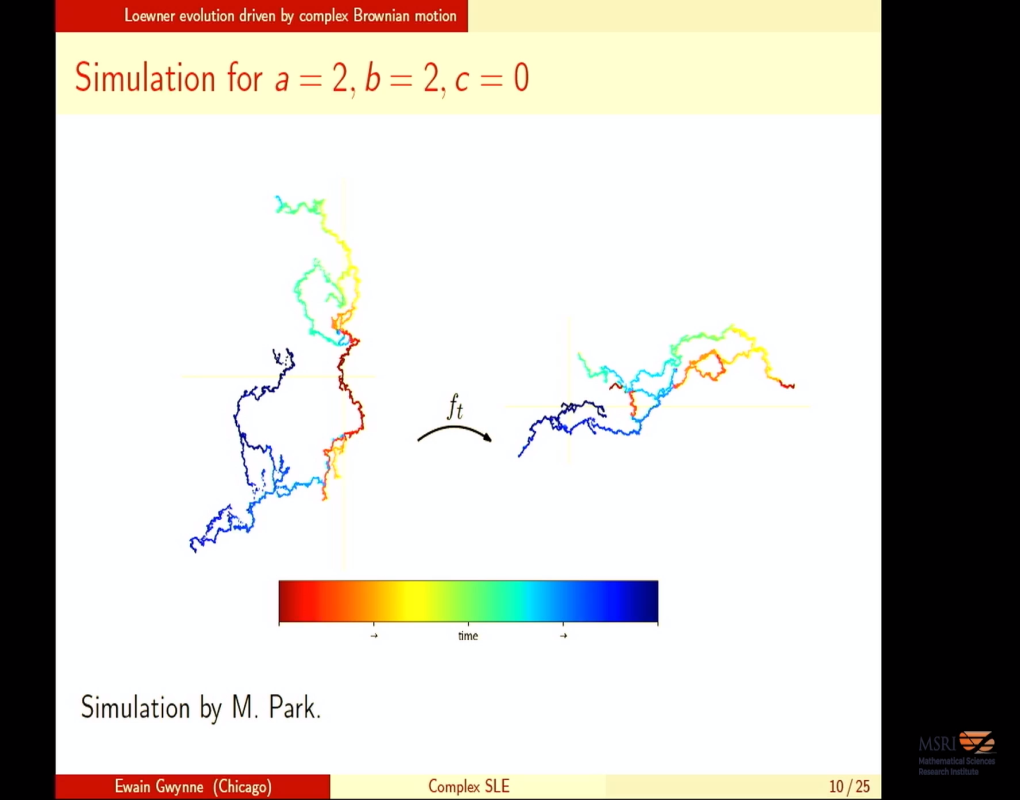
We consider the Loewner evolution whose driving function is $W_t = B_t^1 + i B_t^2$, where $(B^1,B^2)$ is a pair of Brownian motions with a given covariance matrix. This model can be thought of as a generalization of Schramm-Loewner evolution (SLE) with complex parameter values. We show that our Loewner evolutions behave very differently from ordinary SLE. For example, if neither $B^1$ nor $B^2$ is identically equal to zero, then the complements of the Loewner hulls are not connected. We also show that our model exhibits three phases analogous to the phases of SLE: a phase where the hulls have zero Lebesgue measure, a phase where points are swallowed but not hit by the hulls, and a phase where the hulls are space-filling. The phase boundaries are expressed in terms of the signs of explicit integrals. These boundaries have a simple closed form when the correlation of the two Brownian motions is zero. Based on joint work with Josh Pfeffer, with simulations by Minjae Park.