Abstract
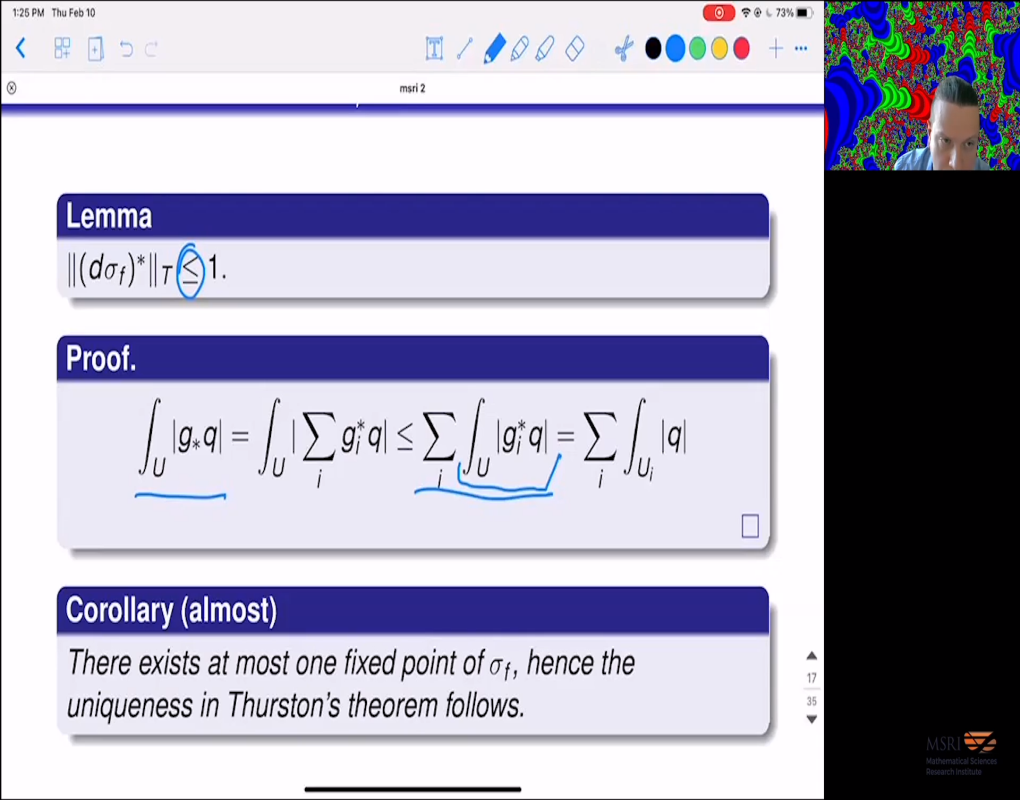
Thurston's theorem states that a post-critically finite branched self-covering of a sphere is combinatorially equivalent to a rational map if and only if it does not admit a certain kind of topological obstruction. The proof of the theorem uses iteration on the Teichmueller space, the so-called Thurston pullback map, to find an invariant complex structure. In the obstructed (and non-parabolic) case, the map diverges to the stratum at infinity associated with the canonical obstruction of the map. We will review properties of the Thurston pullback map and discuss its relation to the twisting problem of branched self-coverings of the sphere and other applications.