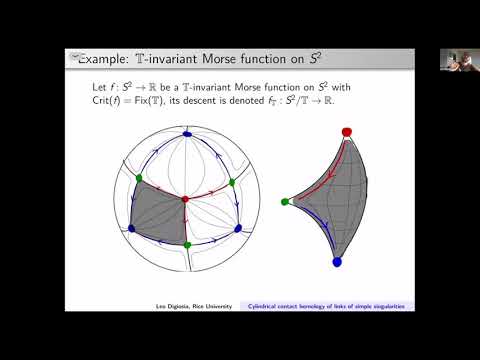
In this talk we consider the links of simple singularities, which are contactomoprhic to S3/G for finite subgroups G of SU(2,C). We explain how to compute the cylindrical contact homology of S3/G by means of perturbing the canonical contact form by a Morse function that is invariant under the corresponding rotation subgroup. We prove that the ranks are given in terms of the number of conjugacy classes of G, demonstrating a form of the McKay correspondence. We also explain how our computation realizes the Seifert fiber structure of these links.