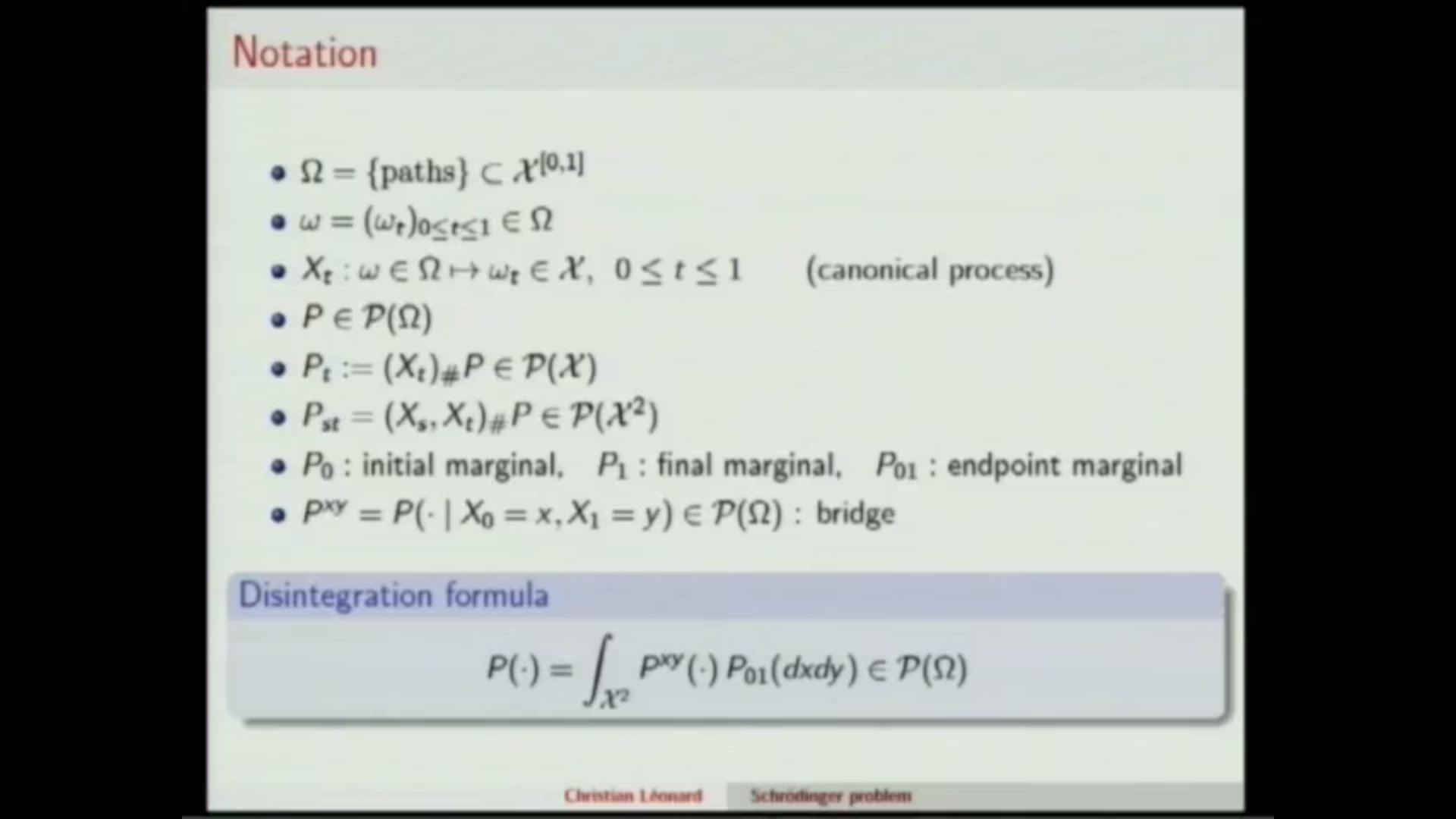
To fit in with the spirit of an introductory workshop, the first part of the talk intends to be expository. The final part will be devoted to some advanced results about discrete metric graphs. In 1931, Schrödinger addressed a problem of statistical physics nature which amounts to minimize the relative entropy of Markov random processes on a state space X subject to prescribed initial and final marginal distributions. The time marginal flow of the minimizing Markov process interpolates between the prescribed marginals on the space Proba(X) of probability measures on X. Large deviations arguments show that slowing the processes down towards a no-motion process leads to a dynamical Monge-Kantorovich problem whose transport cost function is related to the random dynamics. The corresponding entropic interpolations are smooth paths on Proba(X) which converge to some displacement interpolation. For instance, if one takes the Brownian motion as reference process, the limiting interpolation is McCann's one. Considering random walks on a discrete set X with a graph structure and passing to the slowing down limit allows to define natural displacement interpolations on Proba(X) that are geodesics with respect to an intrinsic graph distance. This opens the way for investigating curvature of graphs by tracking Lott-Sturm-Villani theory.