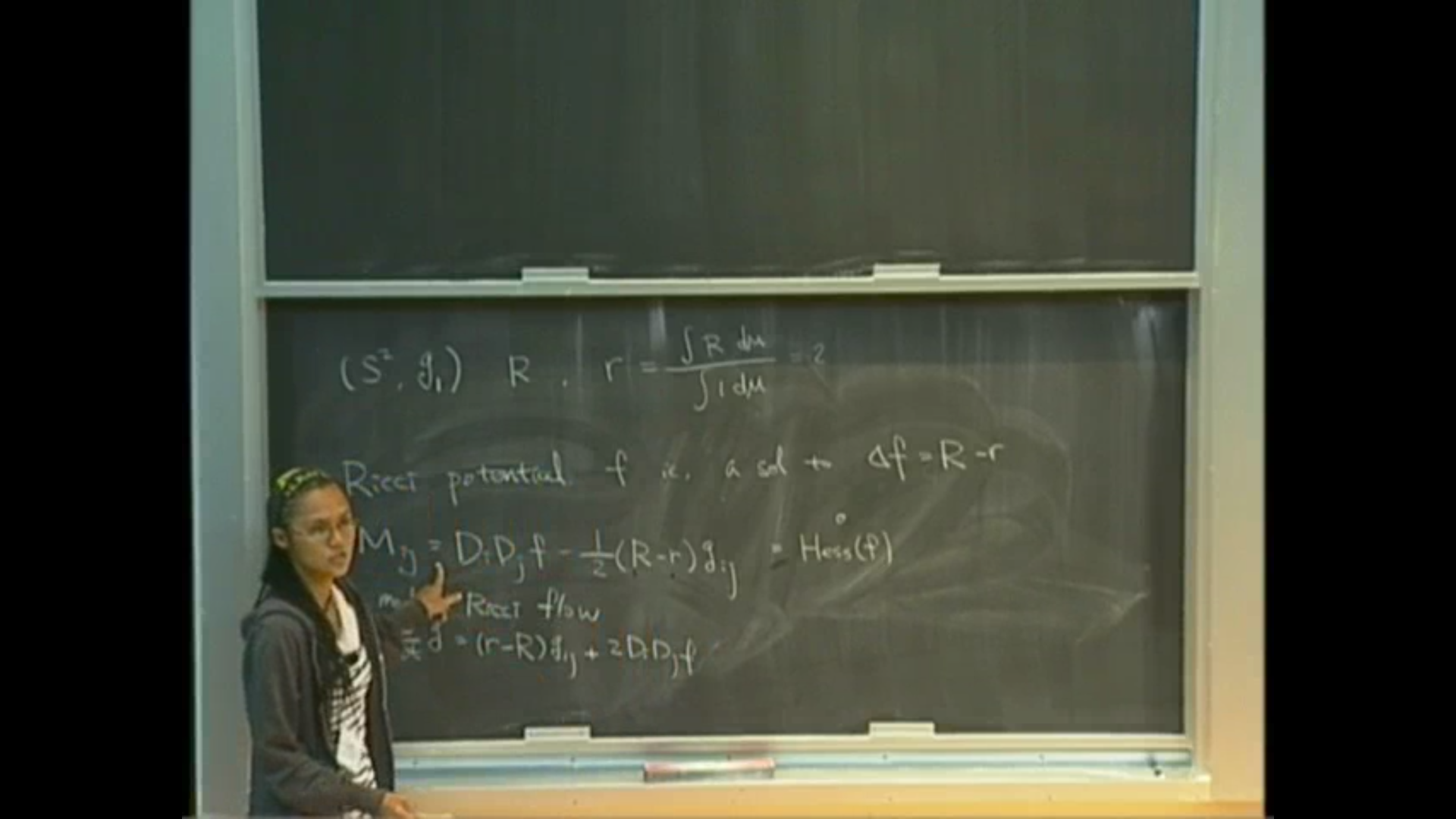On Hamilton’s Ricci flow and Bartnik’s construction of metrics of prescribed scalar curvature
Presenter
September 3, 2013
Keywords:
- mathematical relativity
- PDE and relativity
- differential geometry
- Lorentzian geometry
- Lorentzian manifold
- Einstein equations
- curvature
- Ricci curvature
- Ricci flows
- flat 3-metrics
MSC:
- 83-XX
- 83CXX
- 83C05
- 83C20
- 83C60
- 83C75
- 35Qxx
- 35Q75
- 35Q76
- 53C44
Abstract
Riemannian 3-manifolds with prescribed scalar curvature arise naturally in general relativity as spacelike hypersurfaces in the underlying spacetime. In 1993, Bartnik introduced a quasi-spherical construction of metrics of prescribed scalar curvature on 3-manifolds. This quasi-spherical ansatz has a background foliation with round metrics and converts the problem into a semi-linear parabolic equation. It is also known by work of R. Hamilton and B. Chow that the evolution under the Ricci flow of an arbitrary initial metric $g_0$ on $S^2$, suitably normalized, exists for all time and converges to the round metric. In this talk, we describe a construction of metrics of prescribed scalar curvature using solutions to the Ricci flow. Considering background foliations given by Ricci flow solutions, we obtain a parabolic equation similar to Bartnik’s. We discuss conditions on the scalar curvature that guarantees the solvability of the parabolic equation, and thus the existence of asymptotically flat 3-metrics with a prescribed inner boundary. In particular, many examples of asymptotically flat 3-metrics with outermost minimal surfaces are obtained.