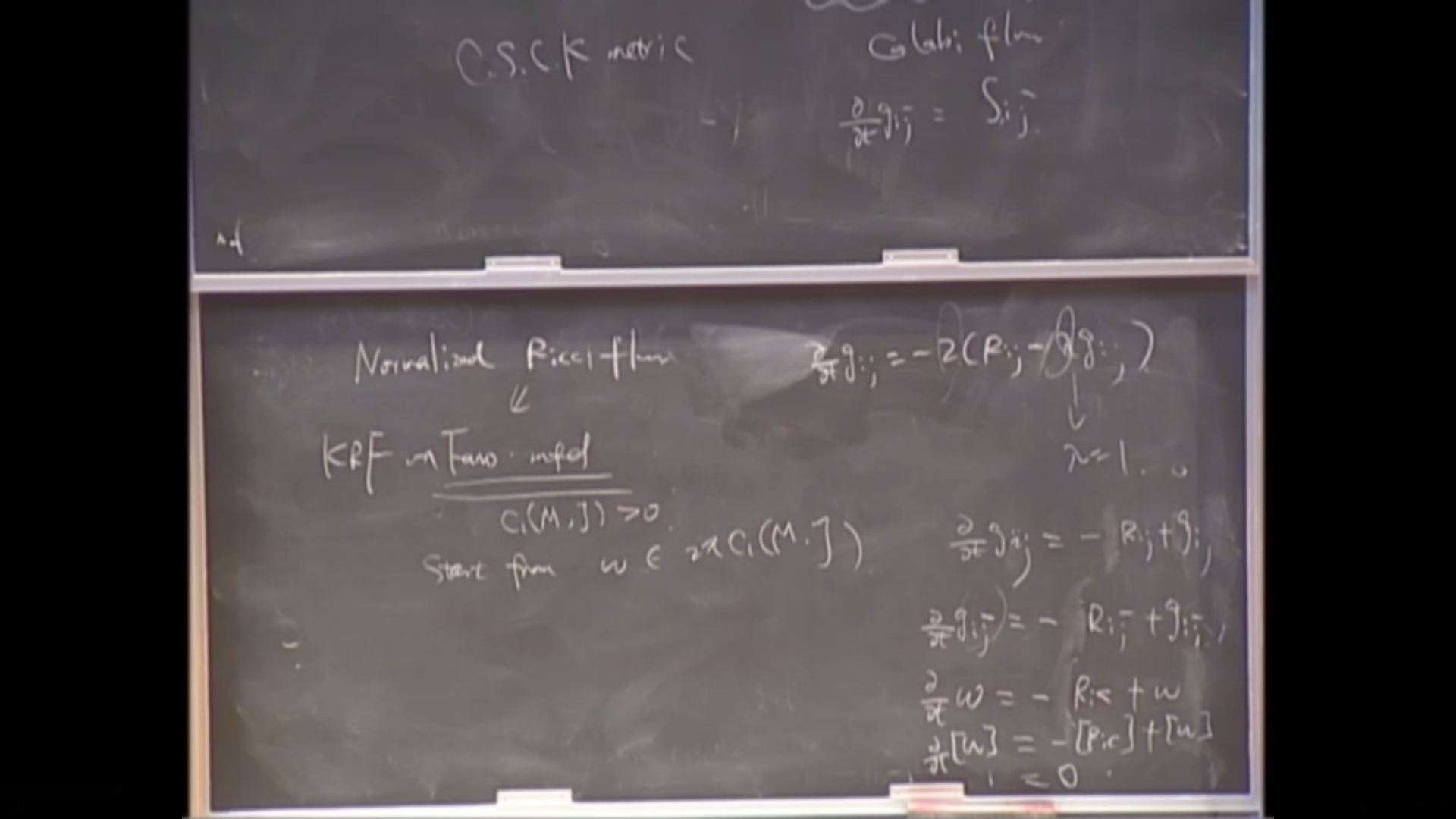Kähler Ricci flow on Fano manifold
Presenter
March 22, 2016
Keywords:
- algebraic geometry and GAGA
- mathematical physics
- complex differential geometry
- Kahler metric
- mirror symmetry
- Calabi-Yau manifold
- Ricci flows
MSC:
- 32Q25
- 53-XX
- 53CXX
- 53C55
- 53C80
- 53Zxx
- 14-xx
Abstract
Based on the compactness of the moduli of non-collapsed Calabi-Yau spaces with mild singularities, we set up a structure theory for polarized K\"ahler Ricci flows with proper geometric bounds. Our theory is a generalization of the structure theory of non-collapsed K\"ahler Einstein manifolds. As applications, we prove the Hamilton-Tian conjecture and the partial-C0 conjecture of Tian.