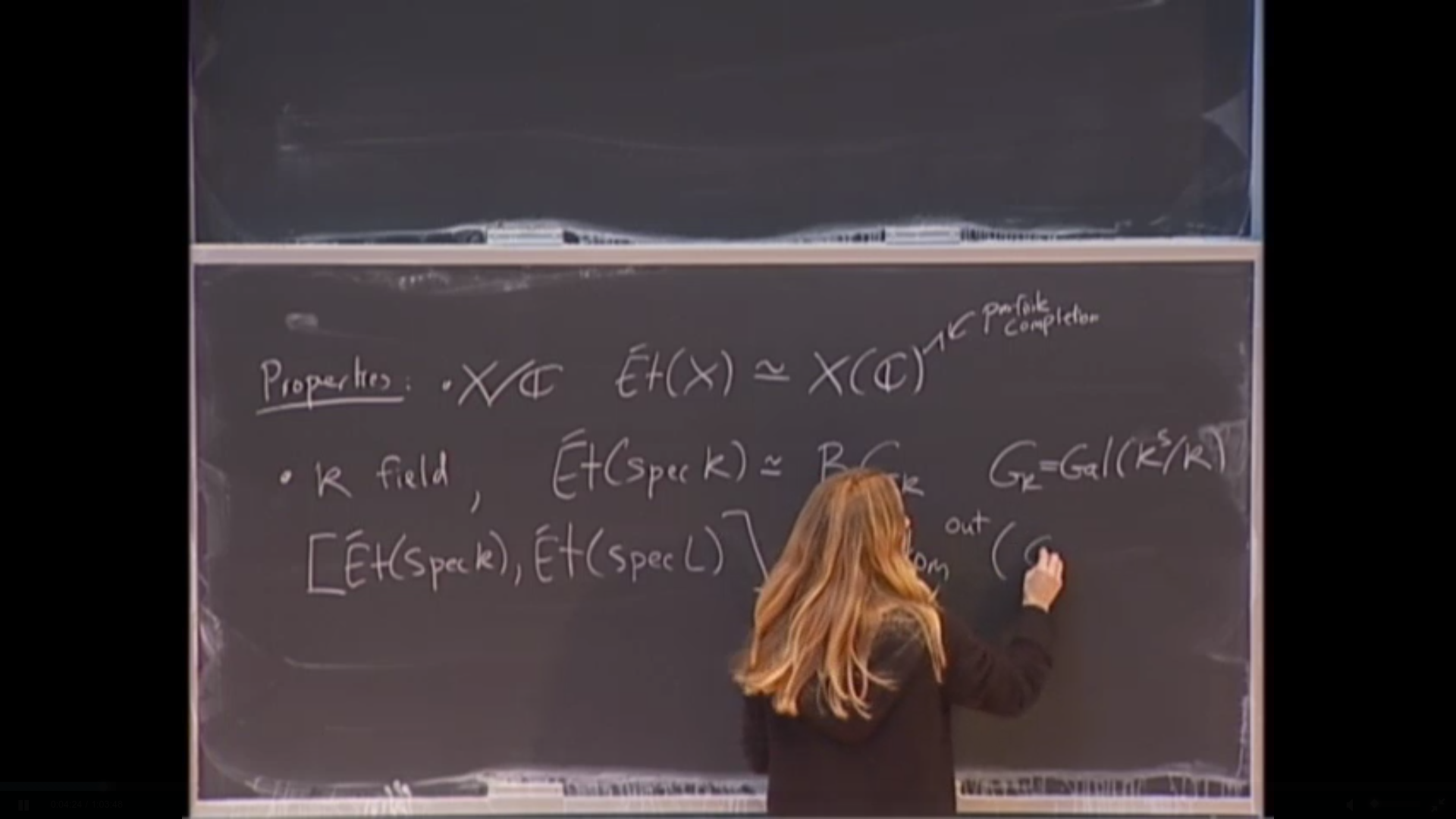The solutions in \mathbb{C} to a system of polynomial equations form a nice topological space which is useful even for studying solutions to the polynomials over smaller fields such as R or even Q. To study solutions over Q or characteristic p fields, it is more useful to replace the notion of topological space with an object in a suitable category where one can do homotopy theory, such as the Morel-Voevodsky category for A^1 homotopy theory, and pro-spaces, where one has the étale homotopy type of a scheme. We will define A^1 homotopy theory, étale topological type, and an étale realization between them of Isaksen. We will use this to discuss Grothendieck's anabelian conjectures and obstructions to solutions to polynomial equations.