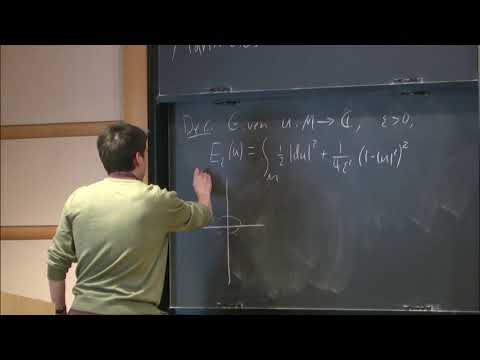We will describe recent progress on the existence theory and asymptotic analysis for solutions of the complex Ginzburg-Landau equations on closed manifolds, emphasizing connections to the existence of weak minimal submanifolds of codimension two. On manifolds with nontrivial first cohomology group, our results rely on new estimates for the Ginzburg-Landau energies along paths of maps connecting distinct homotopy classes of circle-valued maps, which may be of independent interest. As time permits, we will also discuss some key open problems concerning the asymptotic behavior of solutions to the Ginzburg-Landau equations in higher dimensions.