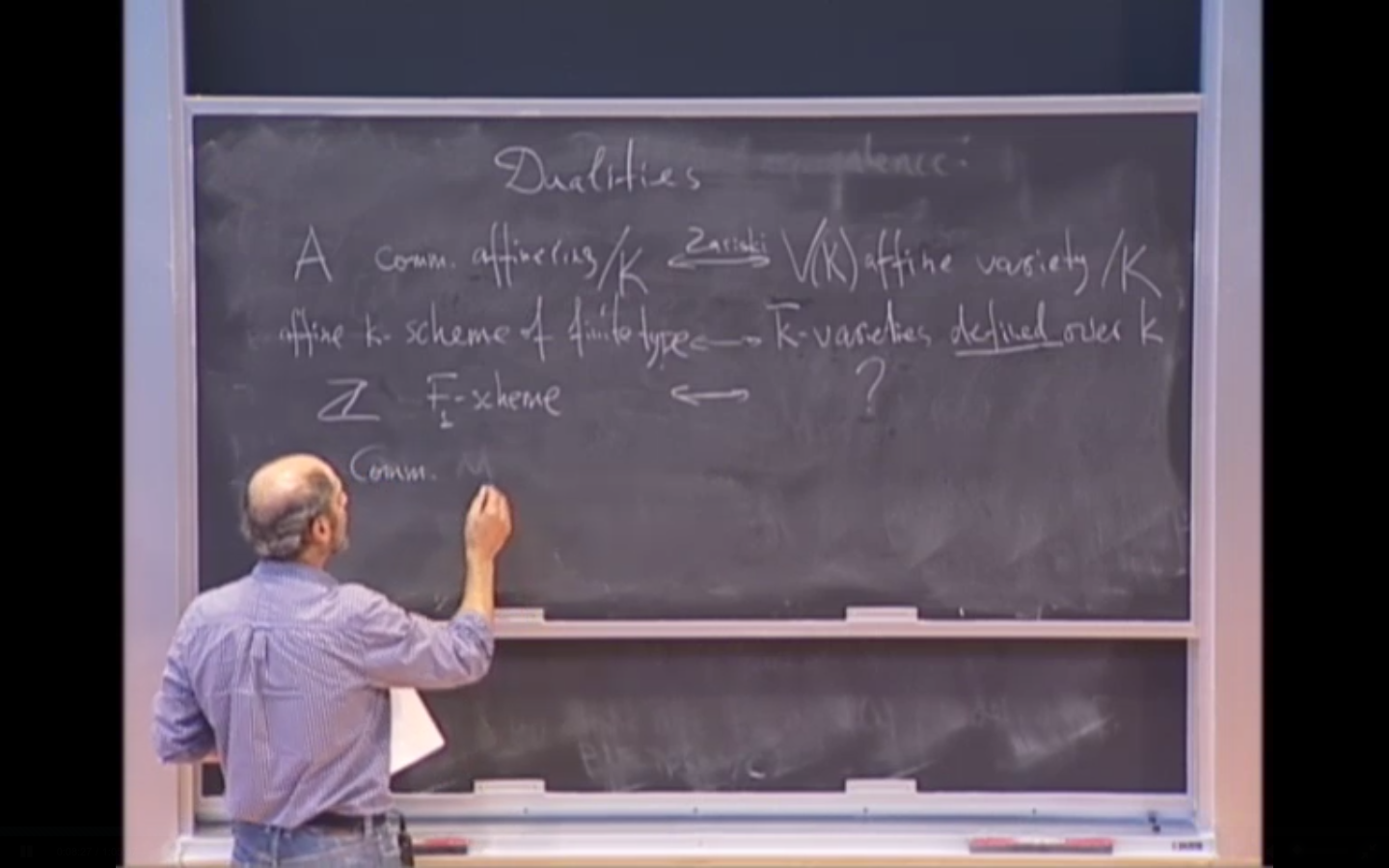On the semantics of non-commutative geometry and exotic summation formulas
Presenter
May 15, 2014
Keywords:
- model theory
- non-commutative geometry
- non-commutative algebras
- Gelfand-Naimark theorem
- duality theorems
- commutative C* algebras
MSC:
- 40Hxx
- 40Jxx
- 46Jxx
- 46J40
- 46J25
Abstract
The well-known duality of classical algebraic geometry between affine varieties and their co-ordinate rings has a perfect analogue in the theory of commutative C^*-algebras, which can be seen by the Gel'fand-Naimark theorem as the algebras of continuous complex-valued functions on a compact Hausdorff space. We interpret this as the Syntax-Semantics duality. In modern geometry and physics one deals with much more advanced generalisations of coordinate algebras, such as schemes, stacks and non-commutative C^*-algebras, where a geometric counterpart is no longer readily available and in many cases is believed impossible.
I will discuss some results of a model-theoretic project which challenges this point of view. This will be illustrated by an application calculating classically non-convergent infinite sum.