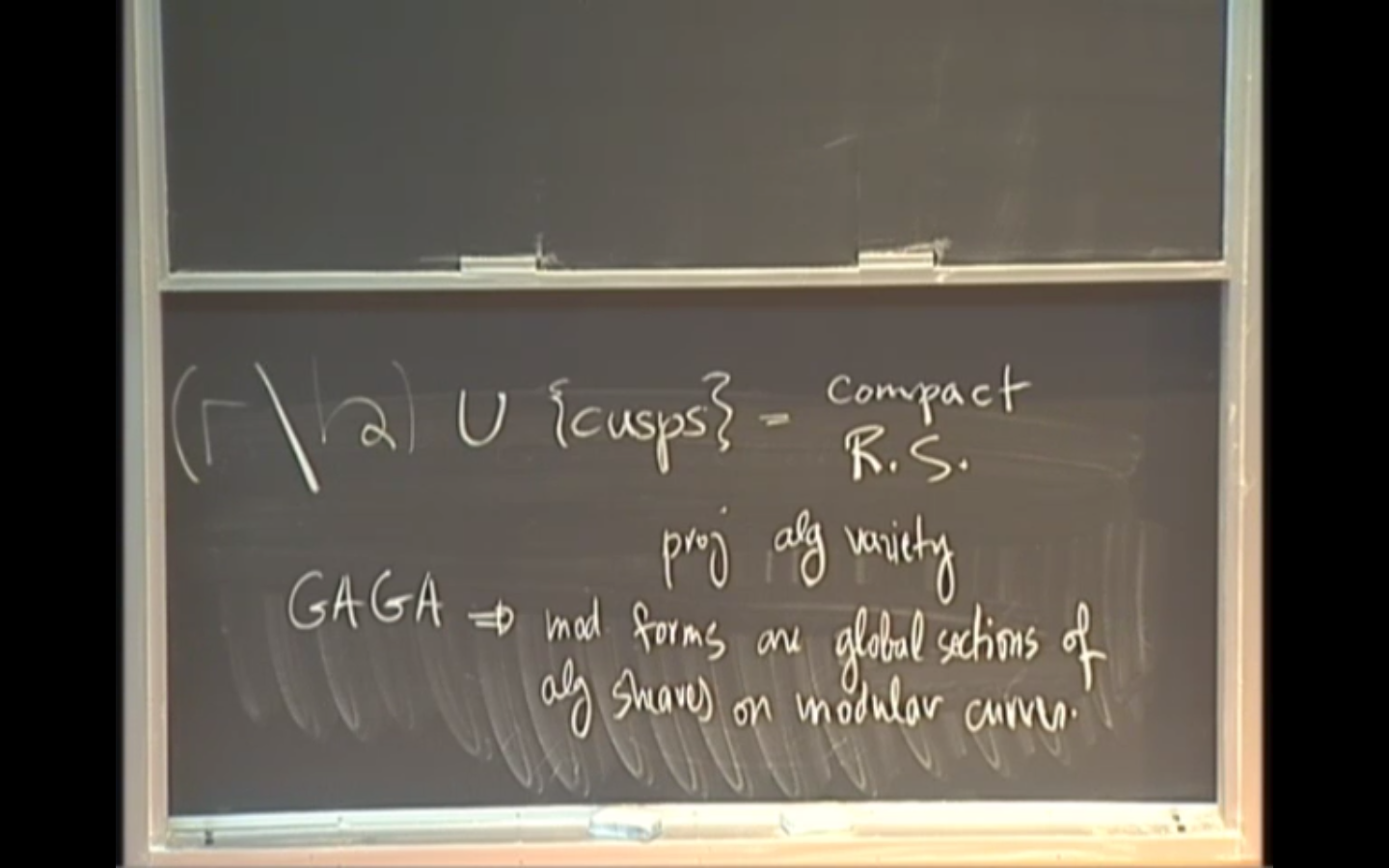Analytic continuation of p-adic modular forms and applications to modularity
Presenter
August 18, 2014
Keywords:
- Galois cohomology
- Galois representation
- GAGA
- p-adic field
- p-adic L-functions
- Riemann surfaces
- uniformization
MSC:
- 11-xx
- 11Fxx
- 11F03
- 11F85
- 11F80
- 11F75
- 11F32
- 11F33
Abstract
The lecture series will start with a brief introduction to rigid analytic geometry. I will then introduce modular curves from various viewpoints (complex analytic, algebraic, and p-adic analytic) and use them to give a geometric definition of p-adic and overconvergent modular forms and Hecke operators. I will next show how to use the p-adic geometry of the modular curves towards p-adic analytic continuation of overconvergent modular forms. Finally, I will demonstrate an application of these results to modularity of certain Galois representations which can itself be used to prove certain cases of the Artin conjecture. If time allows, I would explain briefly how these ideas extend to higher dimensions by illustrating the easier case of Hilbert modular surfaces.