Seung Wook So, an undergraduate participant in ICERM’s Spring 2017 program on “ Singularities and Waves In Incompressible Fluids ,” discovered a proof of a conjecture in the theory of water waves. The question of how steep traveling water waves can become has a long history, going back at least to Stokes [Sto47]. During the ICERM program, So studied the specific question: how steep can traveling water waves get if the water flow has adverse vorticity?  This could occur, for instance, if there is a wind blowing in the opposite (“adverse”) direction to the waves.

Numerical computations in [KS08] indicated that a strong adverse wind would produce very tall and steep waves, but in a weak wind the waves could not get very steep.  So gave the first mathematically rigorous confirmation of the latter conjecture, proving that under small adverse vorticity, the slope of a wave cannot exceed a vorticity-related bound.

During the Spring 2017 ICERM program, So was an undergraduate student at Brown University. He is now pursuing a PhD in mathematics at Princeton University. His result has been published in [SS18]. For further reading, see the references below and the papers cited therein.

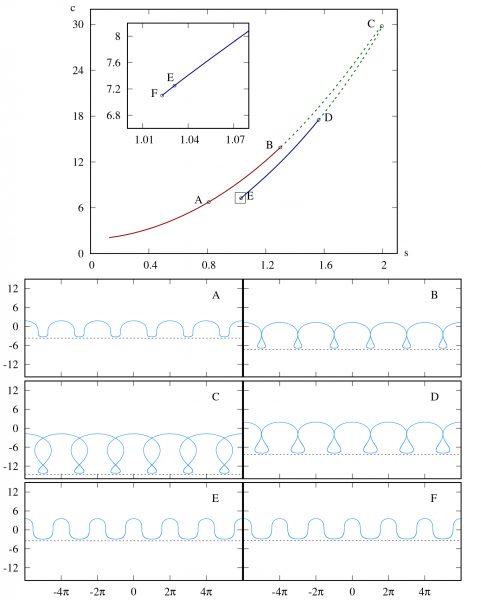
Two other participants in the ICERM program, Sergey Dyachenko and Vera Mikyoung Hur, both of the University of Illinois at Urbana-Champaign, worked independently on the related numerical problem.  They have produced some beautiful computations of wave profiles: see the figures below from [DH18]. The top figure shows a computed continuation curve of wave speed versus steepness for a fixed constant weak adverse vorticity; the inset is a closeup near the endpoint of the continuation. The solid and dashed parts of the curve correspond to physical and non-physical solutions, respectively. The bottom figure shows wave profiles at the indicated points along the curve. Note the “touching” waves at the transitions between physical and non-physical regimes.

REFERENCES
[DH18], S. A. Dyachenko and V. M. Hur, “Stokes waves with constant vorticity: I. numerical computation,” arXiv:1802.07671v1 [physics.flu-dyn] 21 Feb 2018.

[KS08] J. Ko and W. Strauss, “Effect of vorticity on steady water waves,” J. Fluid Mech., 608 (2008), 197-215.

[SS18] S. W. So and W. A. Strauss, “Upper bound on the slope of steady water waves with small adverse vorticity,” J. Differential Equations, 264 (2018), 4136-4151.

[Sto47] G. G. Stokes, “on the theory of oscillatory waves,” Trans. Cambridge Philos. Soc., 8 (1847), 441-473.