Understanding and organizing the basic building blocks of mathematics and physics is one of the most natural of scientific endeavors. We do this with the elements in our periodic table, with descriptions of elementary particles, and with many mathematical structures. Perhaps the simplest example is the description of integers is products of primes.

Paul Bruillard, Siu-Hung Ng, Eric C. Rowell, and Zhenghan Wang studied the properties of mathematical structures called modular tensor categories (MTCs). These structures are models for what are called topological phases of matter which occur at near zero temperatures. The authors developed a way of indexing the MTCs by rank (a non-negative integer), and within each rank they proved that there are only a finite number of such objects.

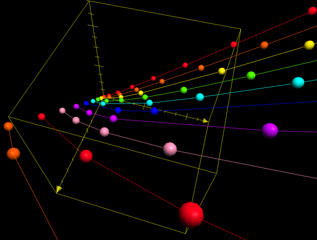
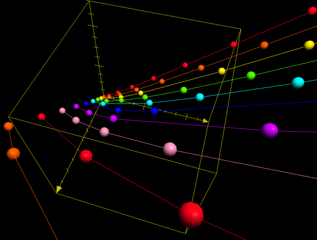
To see how one might prove such a result (but not the actual proof of their result), here is a simple version of the technique. If one considers the equation 𝑎^2+𝑏^2=𝑐^2 and asks for all relatively prime integer solutions, there are infinitely many triples, the Pythagorean triples. But if one requires that 𝑎,𝑏, and 𝑐 only have prime factors from a finite set of primes, then there are only finitely many solutions. This is not obvious, and it is rather difficult to prove. Something similar was carried out for the MTCs. (The figure below shows Pythagorean triples as points in 3-space.)

The joint work of Bruillard, Ng, Rowell and Wang arose from the 2012 AIM workshop “Classifying Fusion Categories” and culminated in the paper “Rank-finiteness for modular categories” published in the Journal of the American Mathematics Society in 2016. For this work, the authors received the 2019 Alexander Award, given by AIM in honor of Gerald Alexanderson, Professor of Mathematics at Santa Clara University. This award recognizes outstanding research articles arising from AIM research activities that have been published within the past three years.

The results in the paper are a wonderful example of the interplay of mathematics and physics and understanding the physical world through the elegance of mathematics. For a more complete description by the authors, please read the full account.