Consider the problem of finding measures that minimize the power sums of absolute values of scalar products on the unit sphere, that is,

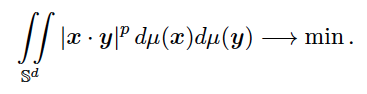
A variant of this problem arises naturally in signal processing: when [math]$p=2$[/math] the minimizers of this energy are precisely isotropic measures, and in the discrete case these are unit norm tight frames (generalizations of the notion of orthonormal basis). Intuitively, the energy in the above expression is minimized by measures [math]$ \mu $[/math] supported on vectors which are “most orthogonal” on the average, however, the realization of this heuristic principle seems to be very different depending on the value of [math]$p$[/math]. For even values of [math]$ p $[/math], the uniform surface measure on [math]$ \mathbb{S}^d $[/math] is a minimizer, and spherical designs (polynomial quadrature rules on the sphere) of order [math]$p$[/math] are discrete minimizers. But for other values of [math]$p$[/math] the situation is much more complicated.

We have established minimizers for some ranges of non-even [math]$ p $[/math] and certain dimensions [math]$ d $[/math]. For example, for [math]$p\in (2,4)$[/math] and [math]$d=2$[/math], the minimizer is supported on the regular icosahedron, while the shortest vectors of the Leech lattice provide the minimizer on [math]$\mathbb{S}^{23}$[/math] for [math]$p\in (8,10)$[/math]. Also, maximal equiangular tight frames (whenever they exist) are minimizers for [math]$p\in (2,4)$[/math] both in the real, and complex cases.

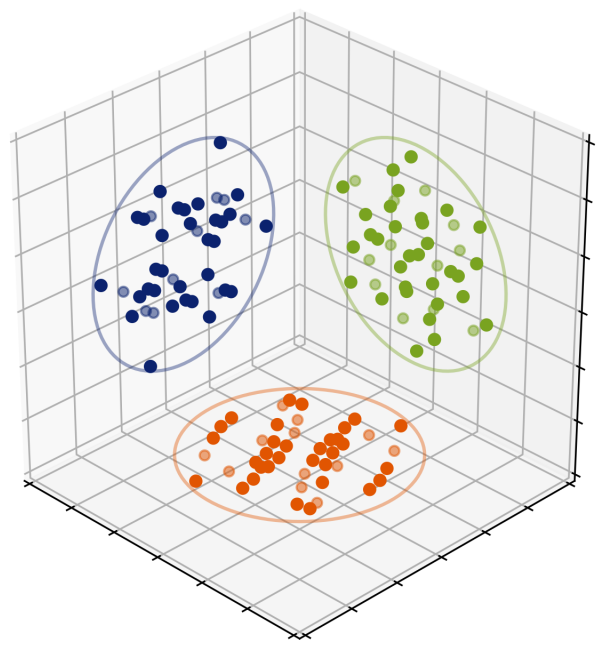
Still, many cases remain mysterious: the work is on-going and we have amassed numerical computations providing potential minimizers: in all cases, the minimizer [math]$ \mu $[/math] seems to have discrete support, and different values of [math]$p$[/math] “pick out” various interesting geometric configurations (some previously known, some new). For example, when [math]$ p=3 $[/math], [math]$ d=5 $[/math], the minimizer likely coincides with the optimal line packing in [math]$ \mathbb{R}^6 $[/math], the three 2-dimensional projections of which are shown above, after a random rotation.

The project is continuing even after the ICERM program, and we expect to uncover new exciting results and connections.

Reported by Dmitriy Bilyk (University of Minnesota) and Oleks Vlasiuk (Vanderbilt University), participants in ICERM’s Spring 2018 Point Configurations in Geometry, Physics and Computer Science semester program.