The subject of cosmology has progressed dramatically in the last 10-20 years. This is illustrated by, among other things, the Nobel prizes in 2006 (cosmic microwave background) and in 2011 (observations of supernovae). In particular, the observations of supernovae led to the unexpected conclusion that the uni- verse is expanding at an accelerated rate. As a result, the currently preferred picture of the universe starts with a big bang, continues with an inflationary phase (a period of very rapid expansion), to then exhibit a slower expansion which transforms into the accelerated expansion observed in the supernovae studies; see the picture below.

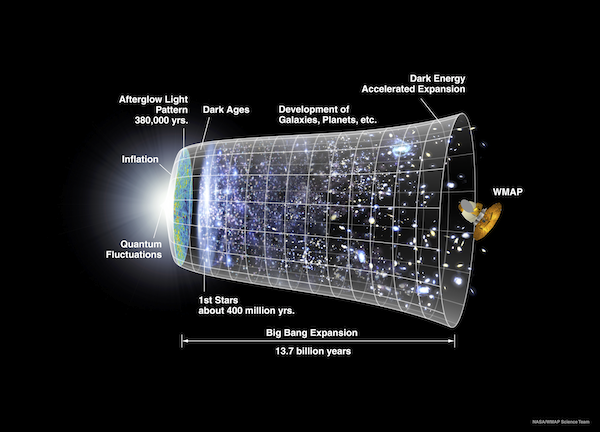
Even though the picture described above fits the observational data quite well, it does give rise to some questions. The standard starting point, on which the above picture is based, is the so-called cosmological principle. This is the assumption that the universe is spatially homogeneous and isotropic; in other words, that, at one moment in time, it is not possible to distinguish between two points in space (homogeneity) nor is it possible to distinguish between two directions (isotropy). These are very strong assumptions, but they are expected to be reasonable on the very large scales relevant in cosmology. On the other hand, it is clear that they are not exactly satisfied. This leads to the mathematical question of stability. In order to explain the origin of this question, it is important to note that Einstein’s equations can be formulated as an initial value problem; given an initial state of the universe, the equations dictate how the universe evolves. The models of the universe used by physicists correspond to initial states which are very special (yielding solutions that are spatially homogeneous and isotropic). It is known that our universe does not correspond to such a highly idealized initial state, but it is expected that it should correspond to a small perturbation of such a state. In this setting, a stability result is a statement of the following kind: if you perturb an initial state corresponding to one of the standard models and evolve the perturbed state using Einstein’s equations, then the resulting solution is globally similar, both in the expanding direction and towards the big bang. Proving stability amounts to justifying the highly idealized models preferred by physicists. It turns out to be possible to prove future stability mathematically, but studying the singularity without symmetry assumptions seems more challenging.

Another question of interest concerns the global shape of the universe. The strong symmetry assumptions described above yield very strong restrictions on the possible shapes. However, due to a mathematical analysis, it turns out to be possible to construct solutions with arbitrary shapes which all observers consider to be practically indistinguishable from the standard model. As a consequence, given the currently preferred models of the universe, the observations do not seem to imply any restrictions.