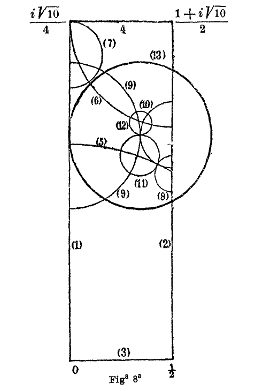
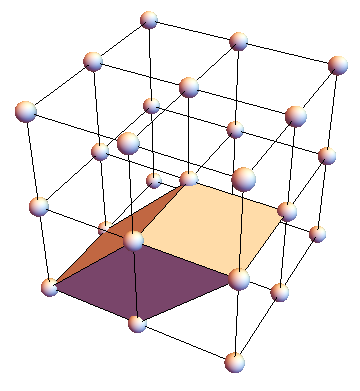
The subject of the special year was locally symmetric spaces.  Examples of these highly symmetric objects are the hyperbolic geometries investigated by Bianchi in the 19th century (the first illustration (on the left) is from Bianchi’s 1893 paper) and a 6-dimensional space parameterizing all possible three-dimensional lattices up to rotation (the second illustration (on the right) shows such a lattice and a fundamental cell for it).

Locally symmetric spaces are the home of the Langlands program, and have become a crossroads for many different strands of mathematical thought.  The current year placed particular focus on two of these strands:

• Analysis on locally symmetric spaces. The motivation to study this comes both from the Langlands program, and from analytic number theory.  The techniques are drawn from representation theory and analysis on manifolds, among other fields.
• Topology of locally symmetric spaces. Here the subject is guided again by a conjecture of Langlands that relates the cohomology of locally symmetric spaces to algebraic varieties.  To understand subtler features of this conjecture was a central theme of the program.

Core program activities.

• There was an introductory short course of six hours, given by Laurent Clozel and Joachim Schwermer.  This series, aimed at an audience with some familiarity with automorphic forms, gave a quick introduction to the cohomology of locally symmetric spaces.
• Research short courses (each a series of two hour lectures) were given by Sasha Goncharov, Yiannis Sakellaridis, Akshay Venkatesh, Romyar Shari, Simon Marshall and Erez Lapid.
  A theme that ran through the lectures of Goncharov, Shari and Venkatesh was an emerging connection between the theory of mixed motives and the theory of automorphic forms, particularly its topological manifestations.  All three hinted at an underlying structure that is only partly visible at present.  The lectures of Marshall, Sakellaridis and Lapid all related to the theory of periods of automorphic forms, and belonged to the analysis side of the program.
• During the second term, there was a “Working group on microlocal analyis and automorphic forms.”  This was a series of lectures or discussions (several by more junior members) on ideas at the interface of the mentioned topics.  This working group seemed to successfully integrate participants of disparate seniority and backgrounds.
• There were two workshops associated to the program, each with 18 research talks:

• Motives, cohomology and Galois representations around the Langlands program , November 6 – November 10, 2017, organized by Frank Calegari and Akshay Venkatesh.

• Representation theory and analysis on locally symmetric spaces , March 5 – March 9, 2018, organized by Erez Lapid, Yiannis Sakellaridis and Akshay Venkatesh.

• There was a great deal of interaction between the program participants and the number theory group at Princeton University. This occurred both through the weekly number theory seminar and yet another “Working seminar.”

Outcomes. There were several important results announced at the program.  Simon Marshall announced a new subconvexity result with Ruixang Zhang that applies in arbitrarily high rank, and Sakellaridis announced in his lecture a new unified approach to relative functoriality, in the spirit of Beyond Endoscopy, that should apply in all rank one cases.  An important function of the program was to seed future growth of the subject.  The lecture series and the working group on microlocal analysis have suggested many new phenomena that seem ripe for further study.  We may hope the future will produce much more activity in these directions.