
Exploiting Combinatorial Regularity for Topological and Morse Measures of ReLU Neural Networks
ICERM - July 2024
by Marissa Masden (University of Puget Sound)
Based on joint work with Robyn Brooks (University of Utah)
The progress of modern machine learning accelerated following the introduction of the Rectified Linear Unit, or ReLU, an extremely simplified model of a neuron that has a max\(\{0,x\}\) “activation” function [1]. For the purposes of this highlight, a ReLU layer is a function \(F_i: \mathbb{R}^{n_{i-1}} \to \mathbb{R}^{n_i}\) of the form \(ReLU \circ A_i\), where the ReLU max\(\{0,x\}\) is applied coordinatewise after an affine function \(A_i\). A (fully connected, feedforward) ReLU neural network is a function composed of ReLU layers of the form:
\(F: \mathbb{R}^{n_0} \xrightarrow{F_1} \mathbb{R}^{n_1} \xrightarrow{F_2} \cdots \xrightarrow{F_m} \mathbb{R}^m \xrightarrow{G} \mathbb{R}\)
where \(G\) is an affine function. In machine learning language, the tuple \((n_0, …,n_m)\) may be thought of as the architecture of the network \(F\). A network learns when the parameters of the affine functions \(A_i\) are updated in training steps via gradient descent, to make \(F\) more closely approximate a target function. Generally, the layer widths \(n_i\) are fixed throughout this process. ReLU neural networks’ advantages include a computationally inexpensive learning rule for updating the \(A_i\) and no gradient-saturation problem like “traditional” sigmoid models [1].
Identifying the capabilities of a machine learning model before applying it is a key goal in neural architecture search [4]. Too small of a model, and the network will never successfully perform its task. Too large of a model, and computational energy is wasted and the cost of model training may become unbearably high. While universal approximation theorems [2] and even dynamics [3] are available for various limiting forms of ReLU neural networks, there are still many questions about the limitations of what small neural networks of this form are capable of accomplishing: for example, what functions may be expressed when the \(n_i\) are fixed and finite? What are the attainable sublevel set topologies when restricting the architecture in this way? Answering these questions can give insight into how many parameters a neural network must have before it is capable of performing a particular task.
Marissa Masden seeks to understand ReLU neural networks through a combinatorial, discrete structure that enables capturing topological invariants of structures like the decision boundary, the \(F(x)= 0\) level set—one way to characterize the classification capability of a network model. Like hyperplane arrangements, ReLU neural networks subdivide their domain \(\mathbb{R}^{n_0}\) into a polyhedral complex. Using language from Grigsby and Lindsey (Boston College), this is called the canonical polyhedral complex corresponding to a given ReLU neural network [5], and it can be thought of as an intersection arrangement of a set of (generally) codimension-1 bent hyperplanes, zero-sets corresponding to individual layers’ affine functions.
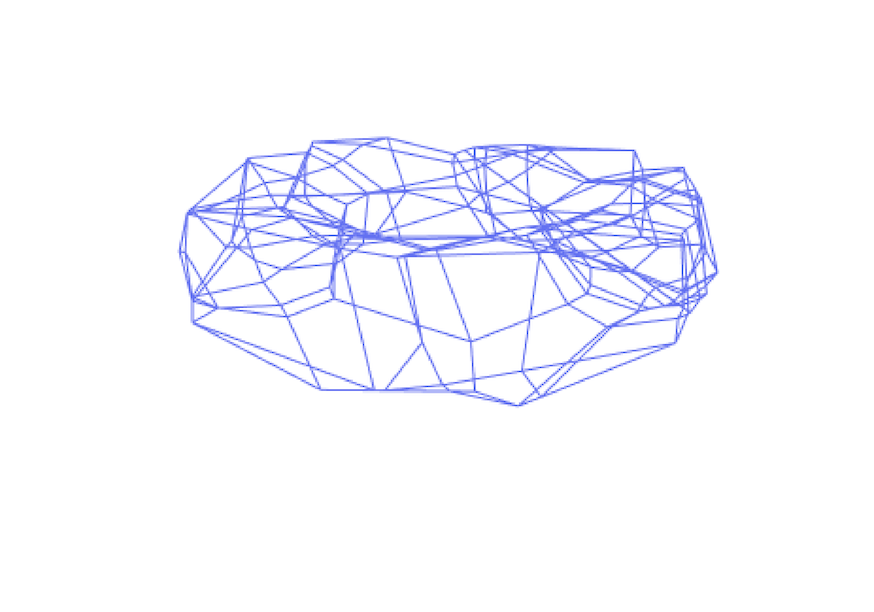
As long as sufficient transversality and genericity conditions are met for the layers, the “bent hyperplanes” corresponding to a ReLU neural network have local \(n_0\)-fold intersections, which are characteristic of hyperplanes in general position [6]. However, globally each “bent hyperplane” may have a seemingly arbitrary combinatorial and topological type, as demonstrated by Figure 1. Despite this, sign vectors in \(\{−1, 0, 1\}^{\sum{n_i}}\) labeling polyhedra with a sign relative to each bent hyperplane—analogous to the covectors of a hyperplane arrangement oriented matroid—are still sufficient to encode the face poset of the polyhedral complex [6]. Furthermore, the sign vectors of only the vertices of the canonical polyhedral complex may be used to reconstruct the connectivity of the entire polyhedral complex.
This combinatorial structure enables the explicit computation of the decision boundary of a classification neural network, the Betti numbers of the decision boundary, the network’s sublevel and superlevel sets, and the piecewise linear (PL) Morse critical points of the function [7]. However, due to the number of vertices growing exponentially in the input dimension \(n_0\), computing the entire polyhedral complex, even only needing vertices and sign vectors, is impractical for networks with even moderately many inputs.
Marissa Masden and Robyn Brooks have developed a local, constructive algorithm for translating between PL Morse functions [8] and Discrete Morse gradient vector fields [9] for ReLU neural networks (depicted in Figure 2), in a bid to identify possible computational and theoretical shortcuts for computing topological expressiveness. In general, such translations may not always be decidable, but in the context of ReLU neural networks the local coordinate axis-like combinatorial structure at each vertex makes the identification of PL critical points, and a translation to a discrete Morse gradient vector field, tractable. Their preprint is forthcoming.
Marissa Masden was an Institute Postdoctoral Fellow at ICERM during the Fall 2023 Math + Neuroscience Semester Program and the Spring 2024 semester. She spent her time there working on this problem, extensions of the described computational tools to alternative neural network architectures, and other projects initiated during the Fall 2023 Semester Program.
References
[1] Vinod Nair and Geoffrey E. Hinton. Rectified Linear Units Improve Restricted Boltzmann Machines. Proceedings of the 27th International Conference on Machine Learning, ICML ’10: 807–814. Omnipress, Madison WI, 2010.
[2] Changcun Huang. ReLU Networks Are Universal Approximators Via Piecewise Linear or Constant Functions. Neural Computation, 32(11): 2249–2278, 2020.
[3] Arthur Jacot, Franck Gabriel, and Clement Hongler. Neural Tangent Kernel: Convergence and Generalization in Neural Networks. Advances in Neural Information Processing Systems, 31. Curran Associates, Inc., 2018.
[4] Pengzhen Ren, Yun Xiao, Xiaojun Chang, Po-yao Huang, Zhihui Li, Xiaojiang Chen, and Xin Wang. A Comprehensive Survey of Neural Architecture Search: Challenges and Solutions. ACM Computing Surveys, 54(4), 2021.
[5] J. Elisenda Grigsby and Kathryn Lindsey. On Transversality of Bent Hyperplane Arrangements and the Topological Expressiveness of ReLU Neural Networks. SIAM Journal on Applied Algebra and Geometry, 6(2): 216–242, 2022.
[6] Marissa Masden. Algorithmic Determination of the Combinatorial Structure of the Linear Regions of ReLU Neural Networks, 2022. https://arxiv.org/abs/2207.07696.
[7] J. Elisenda Grigsby, Kathryn Lindsey, and Marissa Masden. Local and Global Topological Complexity Measures of ReLU Neural Network Functions, 2022. https://arxiv.org/abs/2204.06062.
[8] Romain Grunert. Piecewise Linear Morse Theory. PhD thesis, Freie Universität Berlin, 2017.
[9] Robin Forman. A User’s Guide to Discrete Morse Theory. Séminaire Lotharingien de Combinatoire, 48: Art. B48c, 35, 2002.