Imaging medium properties with waves is ubiquitous in geophysical seismic exploration, medical ultrasound diagnostics, non-destructive evaluation and testing of structures, radar and sonar surveying, etc. Most commonly, one obtains an image by probing the medium of interest with wave pulses emitted and recorded by an array of sensors. Typically, the image is based on the reflectivity, a coefficient of the wave equation used to model the scattering of waves in the medium. The reflectivity is unknown and must be determined by inverting the highly nonlinear mapping from the reflectivity to the array data. This nonlinearity makes the imaging problem particularly challenging, especially when nearby reflectors interact with each other to produce multiple scattering, in which the waves bounce off several reflectors before reaching the sensor array.

Many conventional imaging methods ignore this nonlinearity and are based on the Born approximation, in which the reflectivity-to-data mapping is assumed to be linear. The solution of the resulting imaging problem is much easier since the inverse of a linear map is also linear. This simplification comes at a price, though. In particular, the resulting images become corrupted with artifacts in the presence of multiple reflections.

In [1, 2, 3, 4], the authors developed a novel approach to imaging with waves based on model order reduction. In conventional model order reduction, “full” models are replaced by reduced models that preserve the important dynamics of the full system while being substantially cheaper to work with.

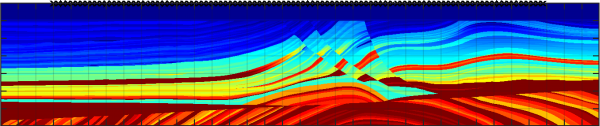
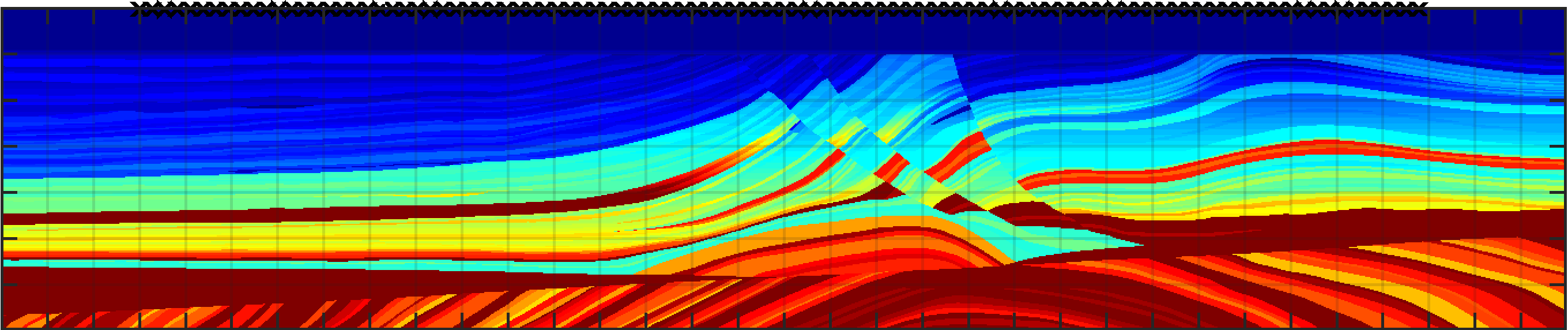
Figure 1: Image for the Marmousi model. Top: true acoustic velocity. Bottom: image obtained directly from the reduced order model. Sensor locations are indicated by ×.

In imaging, however, reduced model construction is complicated by the fact that the full system corresponding to the medium of interest is unknown. This obstacle was first overcome in [1], where a method was proposed for computing reduced models from only the wave data recorded at an array. Once the reduced model is computed from the recorded array data, it can be used in several ways to obtain the desired reflectivity image.

First, the image can be extracted directly from the perturbation of the reduced model relative to the known reference medium, as shown in [2]. In Figure 1 we display an example of such an image for the standard synthetic example in geophysics, the Marmousi model.
Second, the reduced model can be used to transform the multiply scattered measured data to the reflectivity data that would be produced if the propagation of waves in the medium obeyed the Born approximation instead of the true wave equation. This procedure is referred to as the Data-to-Born (DtB) transform [3, 4]. Once the Born data set is obtained from the DtB transform, it can be fed to conventional linear imaging methods, greatly improving their performance since the DtB transformed data is consistent with the linearity assumptions on the reflectivity-to-data mapping. Moreover, the DtB transform is a purely algebraic procedure, which makes it equally applicable to various types of waves, including acoustic, electromagnetic and elastic waves. In Figure 2, we compare the performance of the DtB transform with the true Born approximation data computed for a model of a salt dome protruding through (and deforming) a layered formation (see [4] for details). Both data sets agree to a high degree of precision.

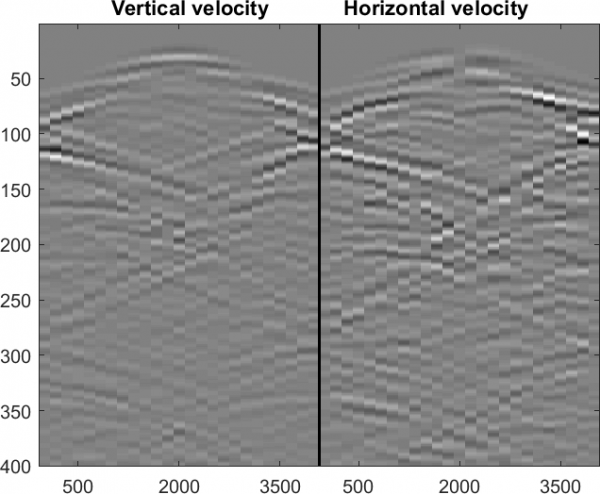
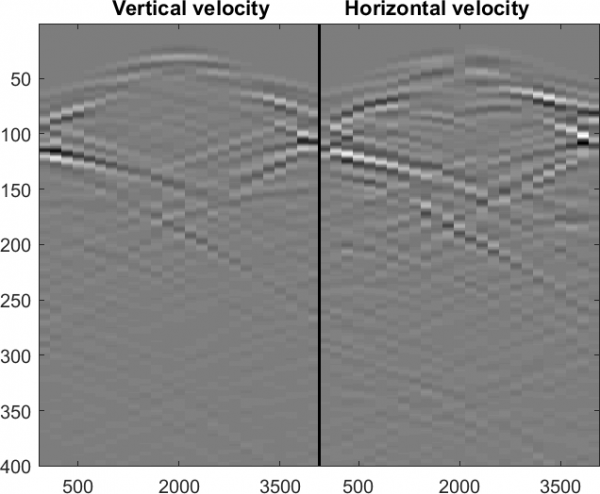
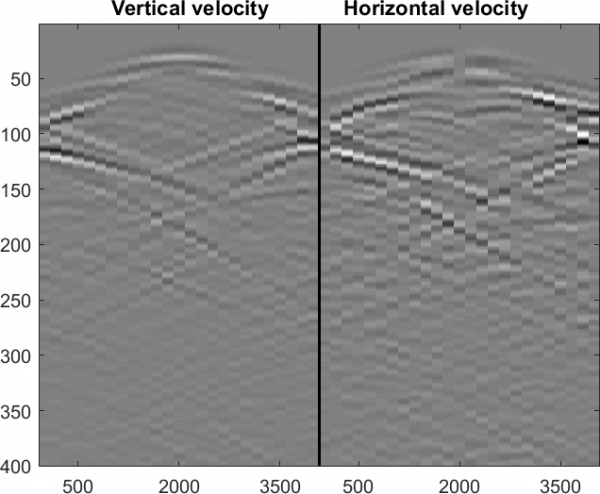
Figure 2: Multiply scattered data (left), the true Born approximant (middle) and the DtB transform (right). The abscissa is location of sensors measuring horizontal and vertical velocity components; the ordinate is the discrete time index.

The project [4] was completed while the authors were in residence at ICERM participating in the Fall 2017 semester program on “ Mathematical and Computational Challenges in Radar and Seismic Reconstruction .”

References
[1] Vladimir Druskin, Alexander V Mamonov, Andrew E Thaler, and Mikhail Zaslavsky. Direct, nonlinear inversion algorithm for hyperbolic problems via projection-based model reduction. SIAM Journal on Imaging Sciences, 9(2):684–747, 2016.
[2] Vladimir Druskin, Alexander V Mamonov, and Mikhail Zaslavsky. A nonlinear method for imaging with acoustic waves via reduced order model backprojection. SIAM Journal on Imaging Sciences, 11(1):164–196, 2018.
[3] Liliana Borcea, Vladimir Druskin, Alexander V Mamonov, and Mikhail Zaslavsky. Untangling nonlinearity in inverse scattering with data-driven reduced order models. Inverse Problems, 34(6):065008, 2018.
[4] Liliana Borcea, Vladimir Druskin, Alexander V Mamonov, and Mikhail Zaslavsky. Robust nonlinear processing of active array data in inverse scattering via truncated reduced order models. arXiv:1805.03747 [math.NA] , 2018.