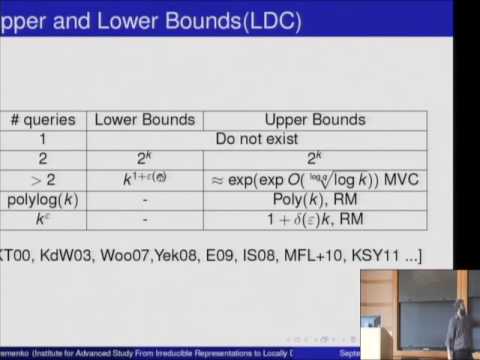
A code C is said to be Locally Decodable Code with q queries if it is possible to recover any symbol x_j of a message x by making at most q queries to C(x), such that even if a constant fraction of C(x) is corrupted, the decoding algorithm returns the correct answer with high probability. LDCs are important not because of their obvious applications to data transmission and data storage but because of their applications to complexity theory and cryptography and Banah spaces. In this talk we will define Locally Decodable Codes and show its connection to the representation theory.