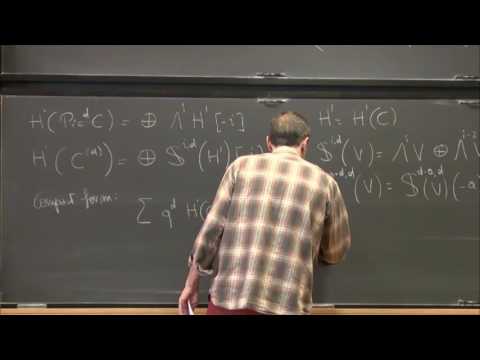I will first discuss a relation between the cohomology groups (with rational coefficients) of the compactified Jacobian and those of the Hilbert schemes of a projective irreducible curve $C$ with planar singularities, which extends the classical Macdonald formula, relating the cohomology groups of the symmetric product of a nonsingular curve to those of its Jacobian. The result follows from a "Support theorem" for the relative Hilbert scheme family associated with a versal deformation of the curve $C$. This approach also defines an important invariant, the "perverse" filtration on the cohomology groups of the Hilbert schemes of $C$. I will then discuss the case $C$ reducible, where a much more complicated relation holds, involving also the compactified Jacobians of partial normalizations of the curve. Work in collaboration with V. Shende and F. Viviani.