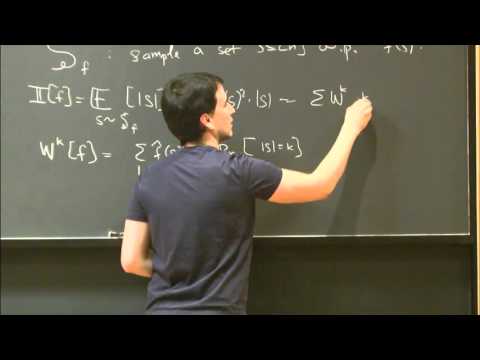The discrete Fourier transform is a widely used tool in the analysis of Boolean functions. One can view the Fourier transform of a Boolean function $f:\{0,1\}^n \to \{0,1\}$ as a distribution over sets $S \subseteq [n]$. The Fourier-tail at level $k$ is the probability of sampling a set $S$ of size at least $k$. We consider Boolean functions whose Fourier-tails have a threshold behavior. That is, above some level $t$, the tails decrease exponentially fast. Several weak classes of Boolean functions have exponentially small Fourier tails: - width-w DNFs, - small-depth circuits, - small-size de-Morgan formulas, and - small-sensitivity Boolean functions We discuss how small Fourier tails are equivalent to moment-bounds and to shrinkage under random restrictions. We plan to mention applications to learning small-depth circuits and to shrinkage of de-Morgan formulas. If time permits, we will prove that small-sensitivity Boolean functions have exponentially small Fourier-tails.