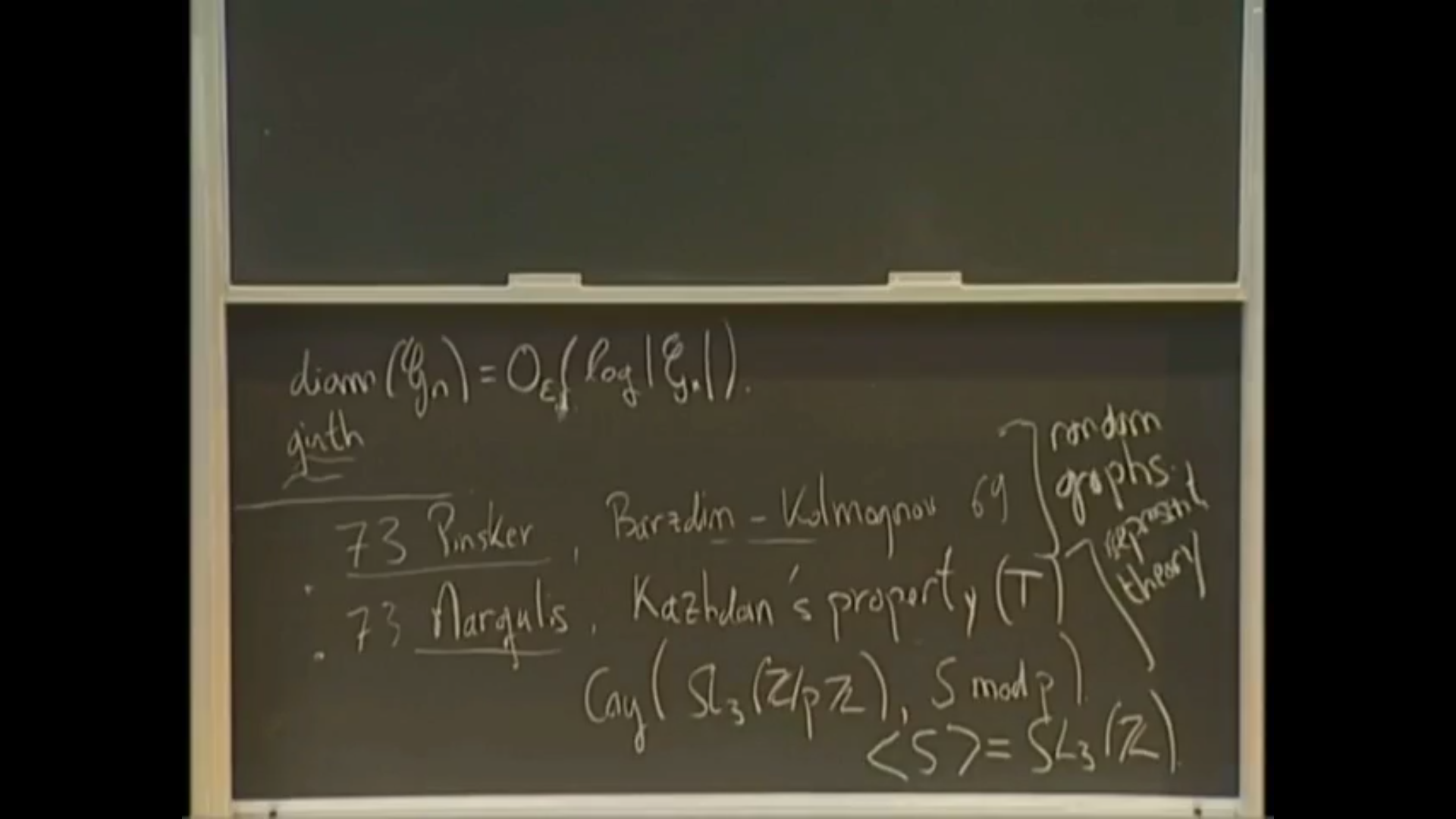In joint work with B. Green, B. Guralnick and T.Tao, we prove that almost all pairs of elements in a finite simple group of bounded rank give rise to a Cayley graph with a uniform spectral gap. The method follows the Bourgain-Gamburd strategy for proving the spectral gap and is based on recent advances in additive combinatorics towards the classification of approximate groups. A key step in the proof is to show the existence of free subgroups of semisimple algebraic groups that are "strongly dense." This means that every non abelian subgroup of it is Zariski dense.