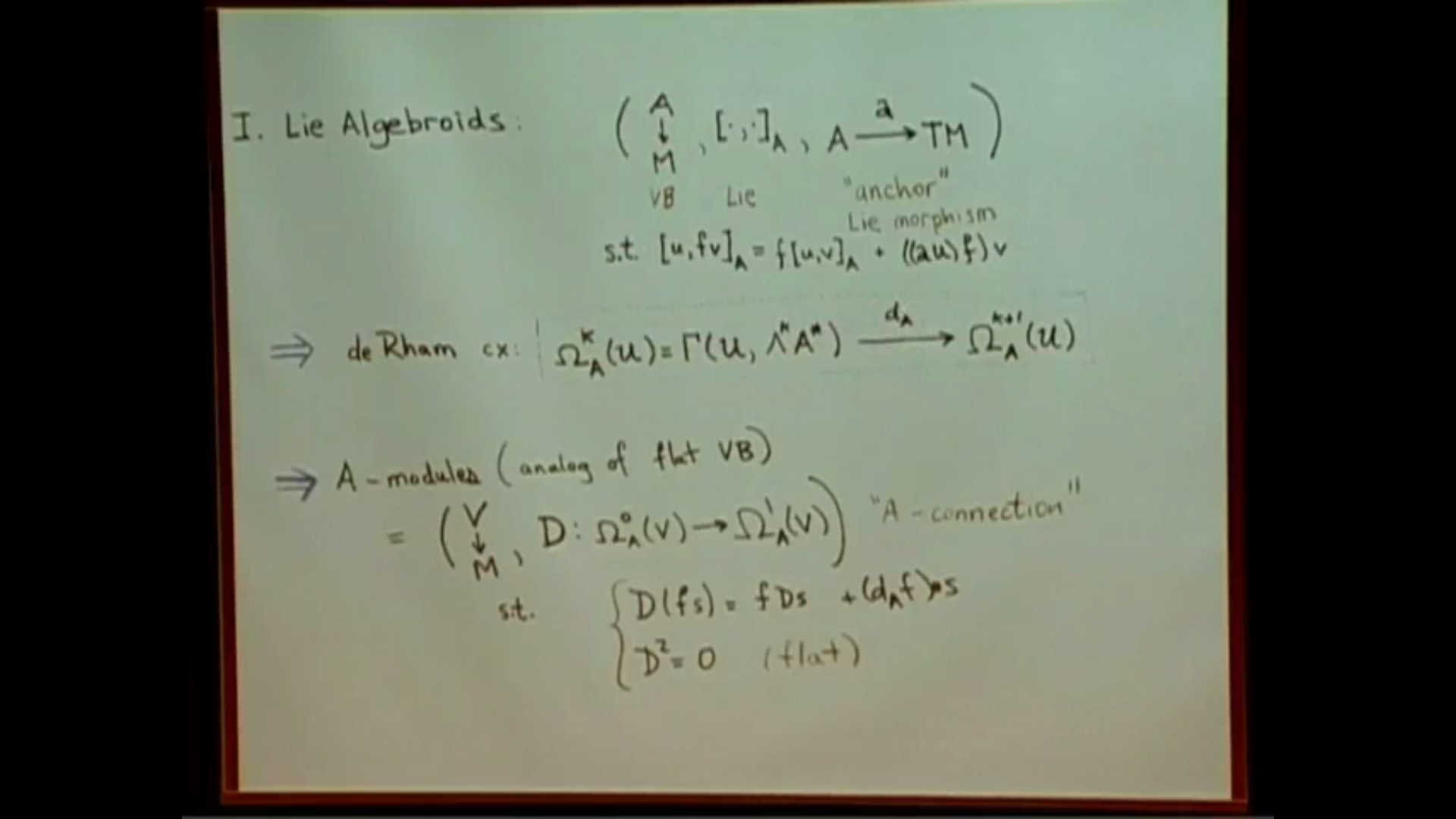On the construction of Lie groupoids
Presenter
November 3, 2011
Keywords:
- Shiing-Shen Chern
- differential geometry
- symplectic geometry
- geometry of stacks
- Lie groupoids and algebroids
- Poisson geometry
- integrable systems
MSC:
- 53-xx
- 17B63
- 53D17
- 53Dxx
- 58H05
- 58H15
- 58H10
- 58Hxx
Abstract
Lie groupoids have a long history in differential geometry, and have become a central object of study in Poisson geometry, in the form of Weinstein's symplectic groupoid associated to an integrable Poisson manifold. In algebraic geometry, they are often used to describe stacks. I will introduce some new constructions of Lie groupoids and elaborate on their significance in Poisson geometry as well as the study of ordinary differential equations. We shall see how classical operations on algebraic surfaces may be employed study groupoids in a similar fashion that we understand the group law on the cubic curve.