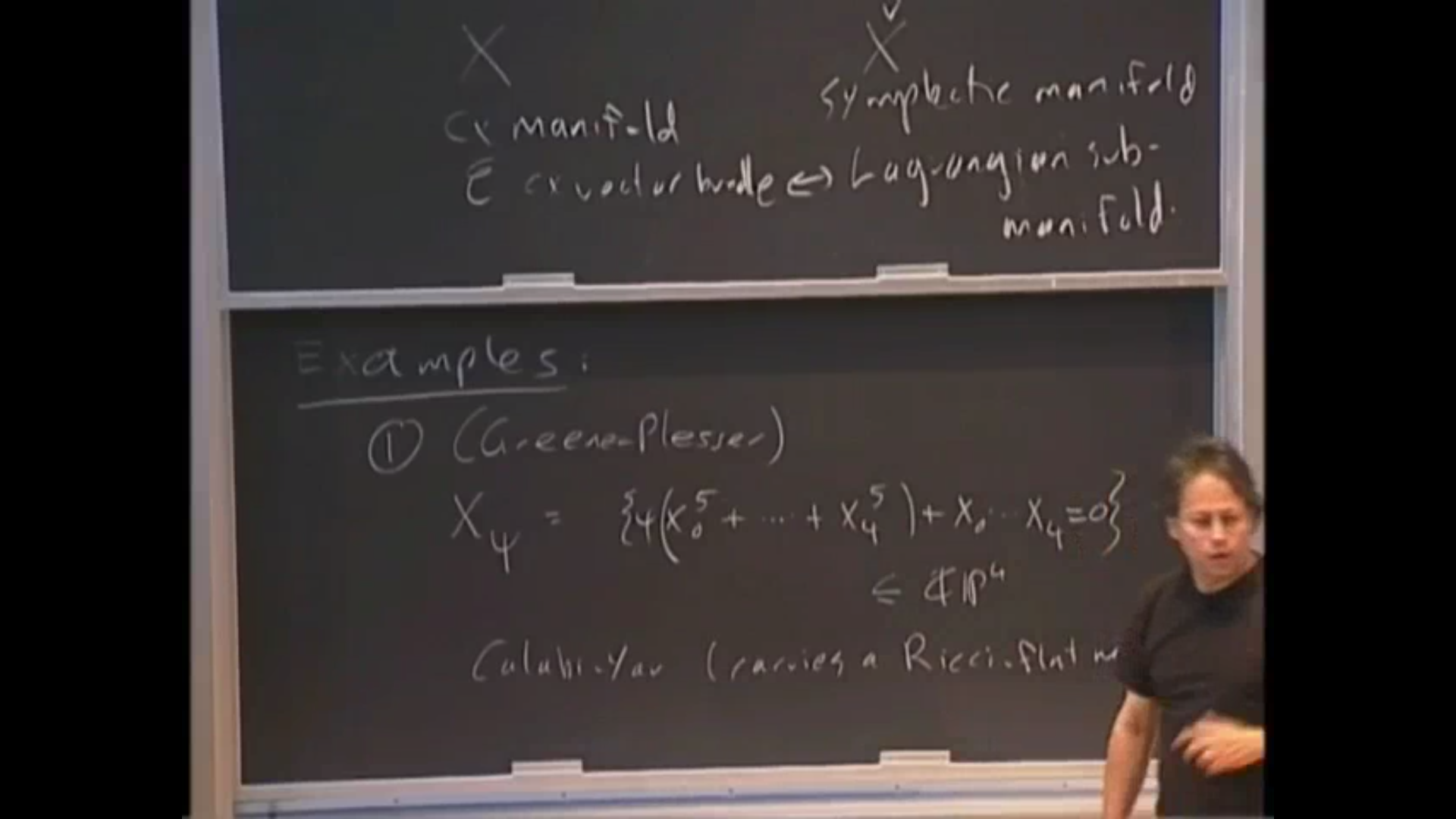I will give an overview of some recent constructions of constant mean curvature surfaces in Riemannian manifolds. I will also review some properties of constant mean curvature surfaces with large mean curvature which, together with the known examples, shed light on the structure of the space of such geometric objects. I will talk about developments in understanding the geometry underlying mirror symmetry over the last 15 years. Starting with the Strominger-Yau-Zaslow conjecture of 1996, the first concrete proposal to understand mirror symmetry geometrically, I will explain how this conjecture, living in the realm of Riemannian geometry, has led to descriptions of mirror symmetry in terms of tropical geometry, a geometry with a very combinatorial flavour.