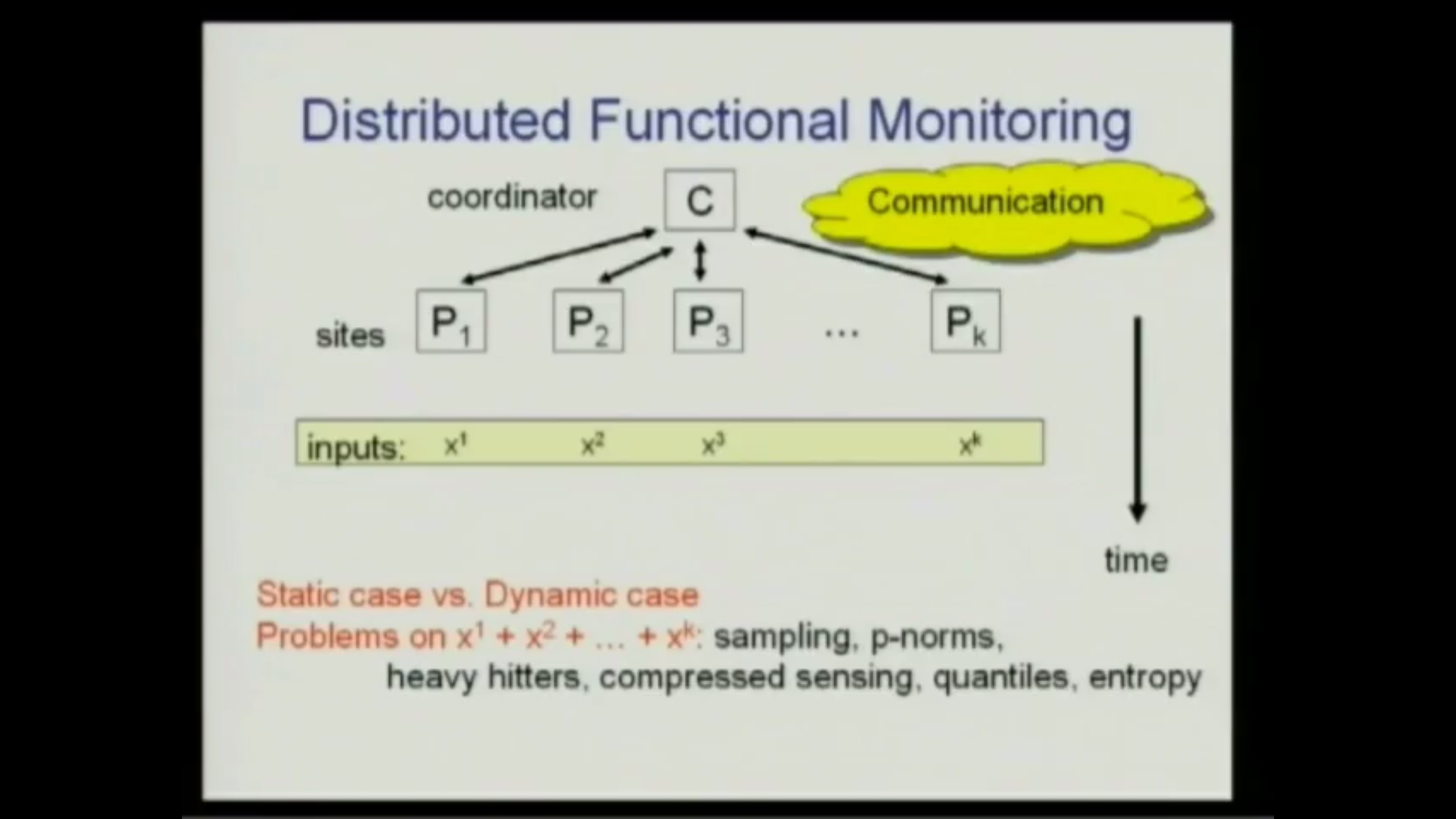
We resolve several fundamental questions in the area of distributed functional monitoring, initiated by Cormode, Muthukrishnan, and Yi (SODA, 2008), and receiving much recent attention. In this model, there are k sites each tracking their input and communicating with a central coordinator. The coordinator's task is to approximately monitor a given function f computed over the union of the inputs continuously, and the goal is to minimize the number of bits communicated. The central problems in this model are the frequency moments (the p-th power of the l_p- norm), heavy hitters, and empirical entropy. For estimating the number of distinct elements F_0, we improve the previous Omega(k + 1/eps^2) bound to a tight Omega(k/eps^2) bound. For the frequency moments F_p, p > 1, we improve the previous Omega(k + 1/eps^2) bound to Omega(k^{p-1}/eps^2). We obtain similar improvements for heavy hitters, empirical entropy, and other problems. Our lower bounds are the first of any kind in distributed functional monitoring to depend on the product of k and 1/eps^2. Moreover, the lower bounds are for the static k-party number-in-hand communication model; surprisingly they almost match what is achievable in the dynamic model. We also show that we can estimate F_p, for any p > 1, in O(k^{p-1} poly(1/eps)) communication. This drastically improves upon the previous O(k^{2p+1}N^{1-2/p} poly(1/eps)) bound of Cormode, Muthukrishnan, and Yi for general p, and their O(k^2/eps + k^{1.5}/eps^3) bound for p = 2. For p = 2, our bound resolves their main open question. Our lower bounds are based on new direct sum theorems for approximate majority, and yield significant improvements to classical problems in the standard data stream model. First, we improve the known lower bound for estimating F_p, p > 2, in t passes from Omega(n^{1-2/p}/(eps^{2/p} t)) to Omega(n^{1-2/p}/(eps^{4/p} t)), giving the first bound that matches what we expect when p = 2. Second, we give the first lower bound for estimating F_0 in t passes with Omega(1/(eps^2 t)) bits of space that does not use the hardness of the gap-hamming problem. Third, we observe an information cost lower bound for the gap-hamming problem, resolving Question 25 in the Open Problems in Data Streams list from the Bertinoro and IITK workshops, and we demonstrate several applications of this fact. Joint work with Elad Verbin and Qin Zhang.