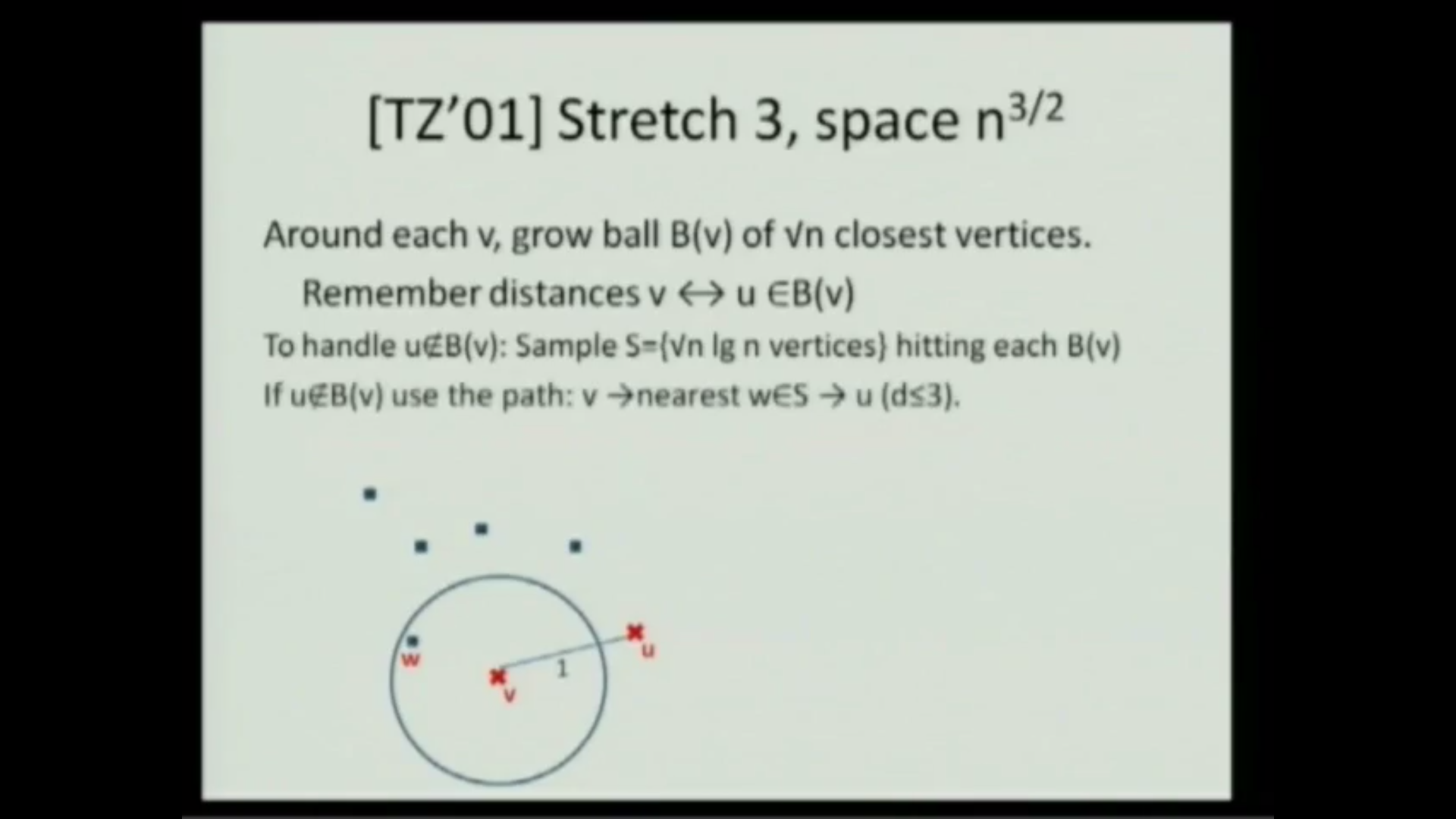
We have known since [Matousek 1996] that any finite metric can be embedded into ell_1 of dimension O(n^{1/k}) with distortion 2k-1. Algorithmically, this is interesting because it gives us a way to represent all pairwise shortest paths in a weighted graph in space much less than n2 (allowing some stretch). A realization of this idea is provided by the famous distance oracle of Thorup and Zwick, which can process any weighted graph into a data structure of size n^{1+1/k} that answers in constant time pairwise distance queries with stretch 2k-1. In other words, they allow distance queries of stretch alpha, but guarantee space n^{1+2/(alpha+1)}. Assuming the girth conjecture, Matousek's embedding is optimal, and so is the Thorup-Zwick distance oracle (for dense enough graphs). Recently, interest has shifted towards sparse unweighted graphs. In this problem, S(alpha) is the (superlinear) space of a data structure that answers approximate distance queries in constant time. Here a denser family of stretches is achievable. In addition to the odd integers, it is possible to implement any stretch alpha \in {2k-1 ± 2/j | k,j naturals} with the same S(alpha) space. I will describe results for this problem, including joint work with Liam Roditty [FOCS'10] or Mikkel Thorup [submitted to STOC'10].