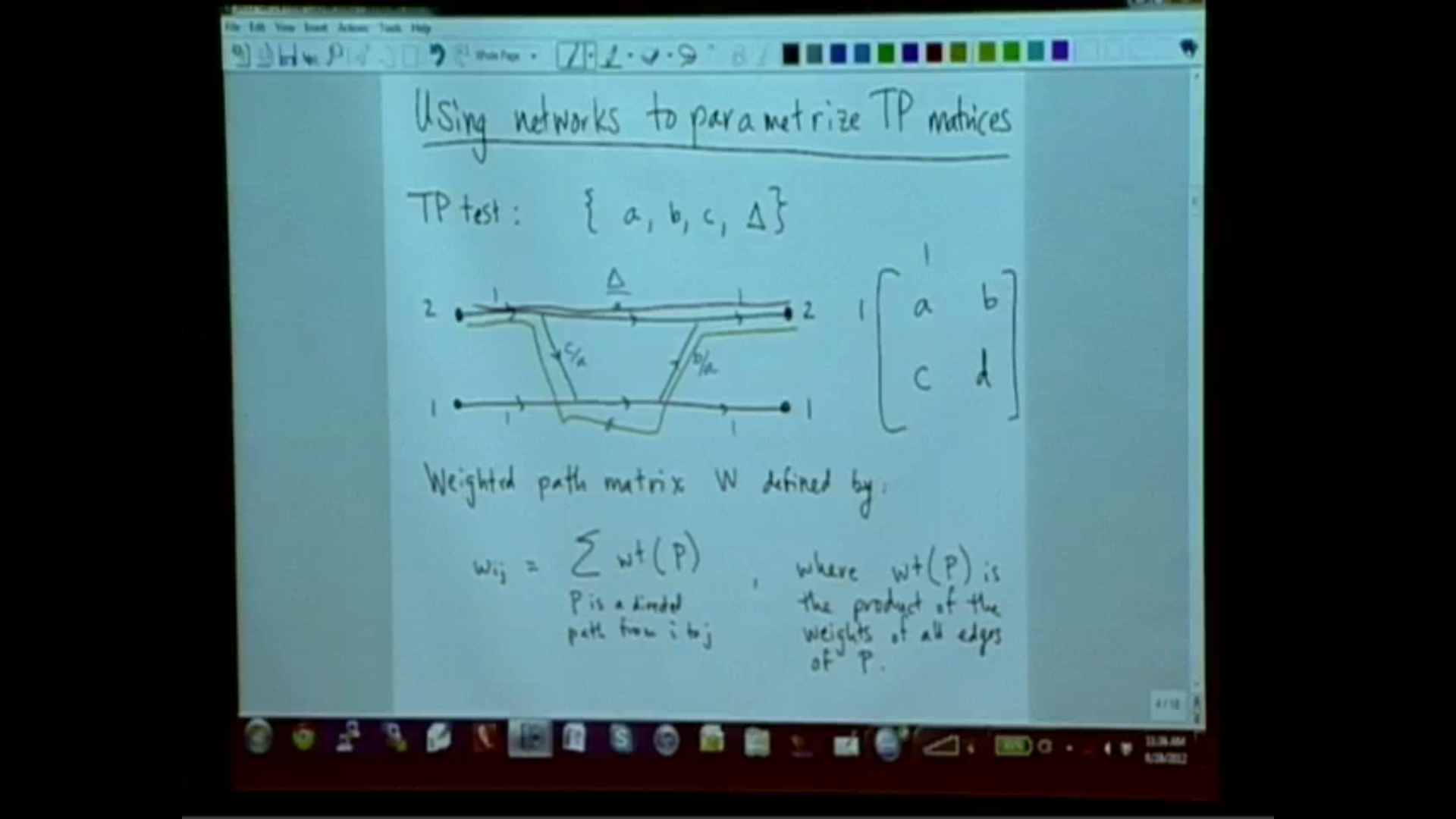
We will discuss some of the combinatorics of the Deodhar decomposition of a real Grassmannian, which is a refinement of Postnikov's positroid stratification, which is in turn a refinement of the Schubert cell decomposition. The positroid strata are indexed by Le-diagrams, and when we consider their intersections with the totally nonnegative part of the Grassmannian, we obtain a nice parametrization of each cell using planar networks, in the sense that each Plucker coordinate can be written as a generating function for certain families of paths in the network. In the Deodhar decomposition, components are indexed by "Go-diagrams", a generalization of Le-diagrams. In this setting, we can also construct a (not necessarily planar) network which parametrizes the corresponding component of the Deodhar decomposition. Thus we obtain a network characterization for the entire Grassmannian. This is a joint project with Lauren Williams.