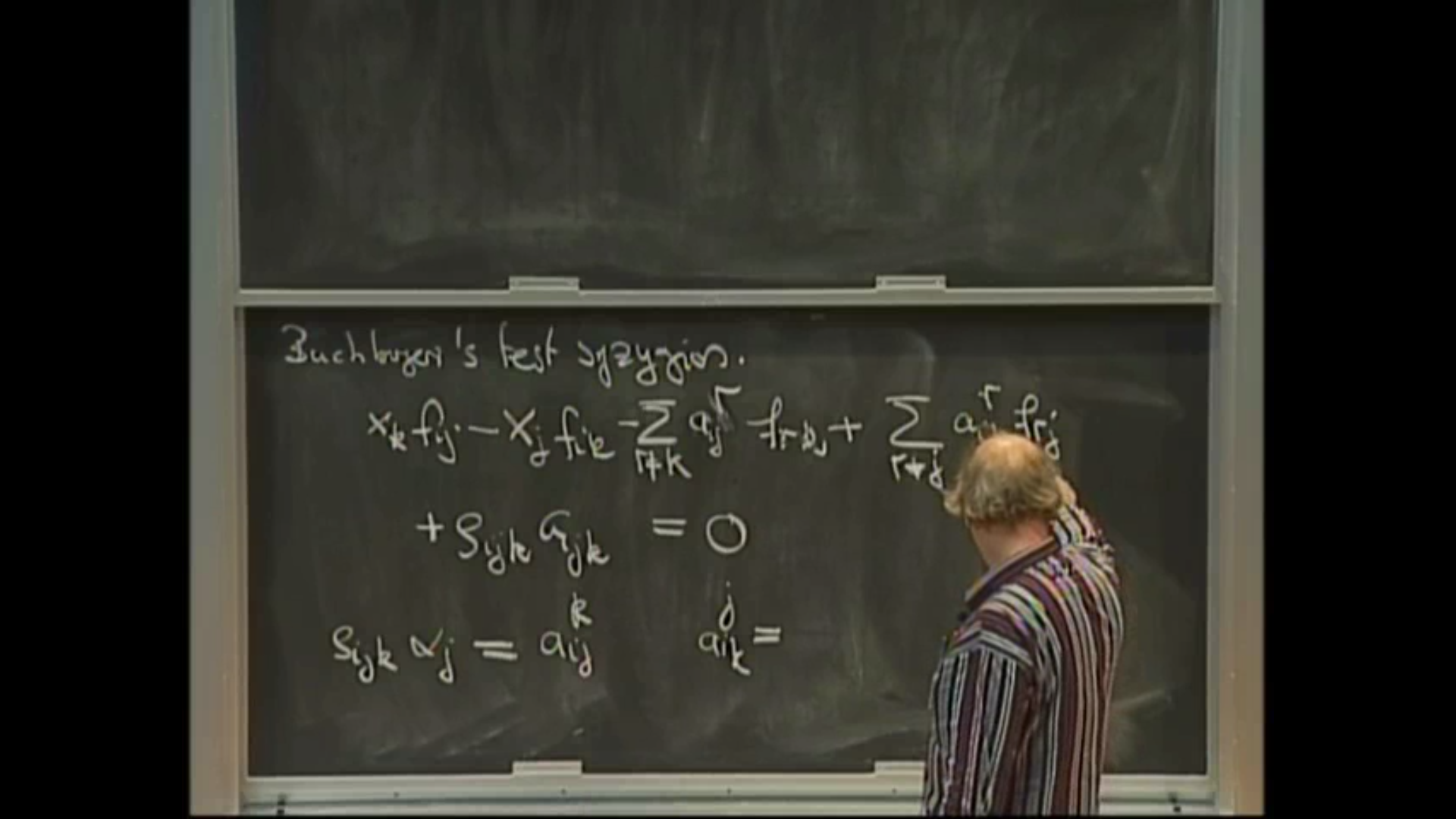The importance of syzygies in algebra was immediately clear after Hilbert proved his syzygy theorem. However computing syzygies remained cumbersome. With the introduction of Gröbner basis and Computer algebra, at least the computation in many interesting examples could be delegate to the Computer, and in the mid-eighties detailed question about the shape of syzygies surfaced. The most prominent example from algebraic geometry is perhaps Green's conjecture on the syzygies of canonical curves. Gröbner basis were introduced by Gordon in his answer to Hilbert's basis theorem. One of the earliest applications of Gröbner basis to syzygies is Petri's analysis about the generation of the homogeneous ideal of a canonical curve. In the first lecture I plan to review the Gröbner basis proof of Hilbert syzygy theorem, and to present Petri's theorem. The second lecture I will recall liaison theory of space curves with the focus on explicit computations. The liaison class of a space curve is characterized by a finite length module, the so called Hartshorne-Rao module. From my point of view, the main difficulty in constructing space curve explicitly, lies in the construction of an appropriate finite length module with desired syzygies. In the final lecture I plan to give some classical unirationality proofs of moduli spaces, now computer aided, and explain how experimental methods can lead to theorems of theoretical interest.