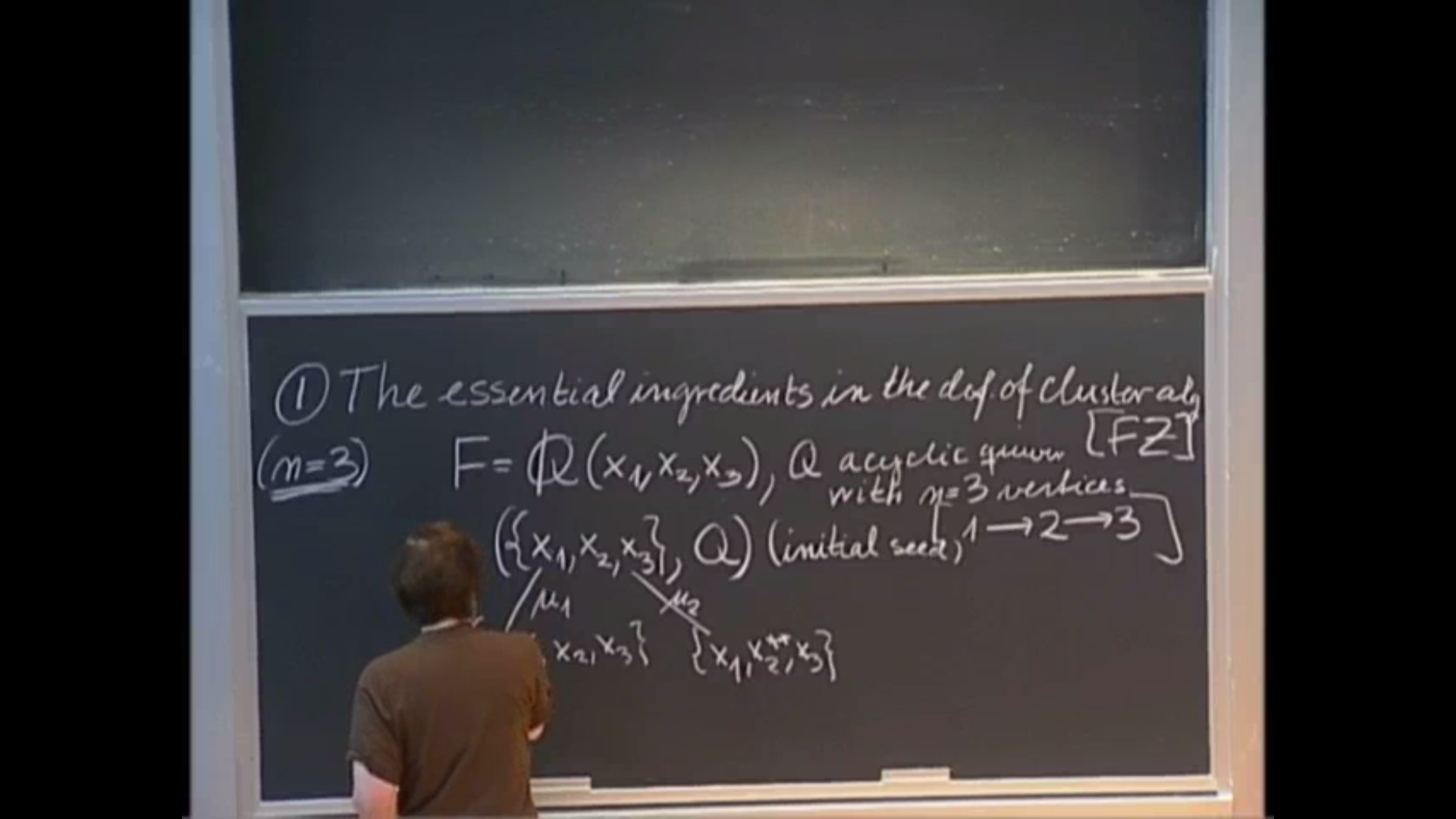Cluster categories #1
Presenter
September 4, 2012
Keywords:
- algebraic combinatorics
- commutative algebra
- cluster algebra
- triangulated category
- Calabi-Yau category
- tilting theory
- quiver representations
- Cohen-Macaulay modules
MSC:
- 13F60
- 13Fxx
- 13-xx
- 05-xx
- 16D90
- 14J32
- 16G20
- 16G60
- 16G70
- 16Gxx
Abstract
We start with introducing the cluster categories associated with finite acyclic quivers (and an algebraically closed field k). Then we define a special class of objects called cluster tilting objects.This theory was motivated by imitating the essential ingredients in the definition of cluster algebras. It is based on the tilting theory for finite dimensional algebras, which we discuss. There is a naturally associated class of algebras, called cluster tilted algebras, and obtained by taking endomorphism algebras of cluster tilting objects in cluster categories.
The cluster categories are Hom-finite triangulated 2-Calabi-Yau. Another important class is the stable categories of preprojective algebras of Dynkin type. Essential properties first developed for cluster categories have been shown to hold in the more general 2-Calabi-Yau setting. This way we also get a more general class of associated finite dimensional algebras.
We consider classes of examples of 2-Calabi-Yau categories, including generalized cluster categories, categories associated with elements in Coxeter groups and some stable categories of maximal Cohen-Macaulay modules over commutative rings. The last class comes from the theory of almost split sequences in the commutative setting. We also discuss relationships between the classes of examples.
These lectures are based on work by many authors.