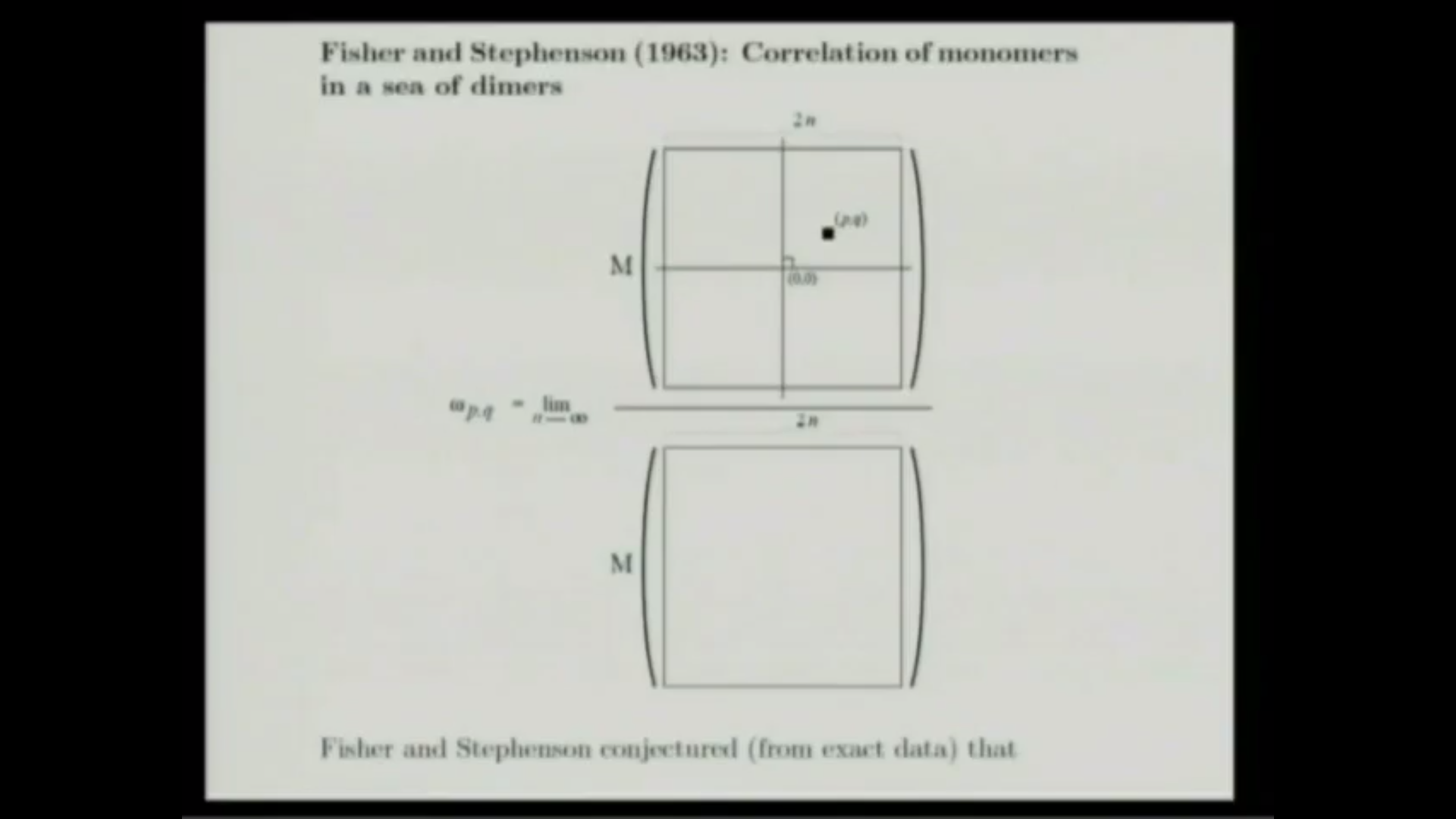
The correlation of gaps in dimer systems was introduced in 1963 by Fisher and Stephenson, who looked at the interaction of two monomers generated by the rigid exclusion of dimers on the closely packed square lattice. In previous work we considered the analogous problem on the hexagonal lattice, and we extended the set-up to include the correlation of any finite number of monomer clusters. For fairly general classes of monomer clusters we proved that the asymptotics of their correlation is given, for large separations between the clusters, by a multiplicative version of Coulomb's law for 2D electrostatics. However, our previous results required that the monomer clusters consist (with possibly one exception) of an even number of monomers. In this talk we determine the asymptotics of general defect clusters along a lattice diagonal in the square lattice (involving an arbitrary, even or odd number of monomers), and find that it is given by the same Coulomb law. We also obtain a conceptual interpretation for the multiplicative constant as the product of the correlations of the individual clusters. In addition, we present several applications of the explicit correlation formulas that we obtain.