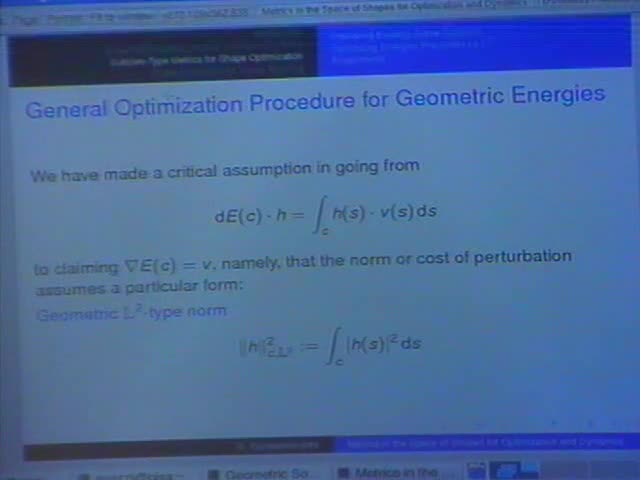
We discuss the use of "geometric" (i.e. formulated exclusively in terms of a curve's arclength parameter) Sobolev metrics to devise new gradient flows of curves. We refer to the resulting evolving contours as "Sobolev Active Contours". An interesting property of Sobolev gradient flows is that they stabilize many gradient descent processes that are unstable when formulated in the more traditional L2 sense. Furthermore, the order of the gradient flow partial differential equation is reduced when employing the Sobolev metric rather than L2. This greatly facilitates numerical implementation methods since higher order PDE's are replaced by lower order integral-differential PDE's to minimize the exact same geometric energy functional. The fourth order L2 gradient flow for the elastic energy of a curve, for example, is substituted by a second order Sobolev gradient flow for the same energy. In this talk we give some background on Sobolev active contours, show some applications using energy regularizers normally connected with fourth order flows, and present some recent results in visual tracking. Joint work with Ganesh Sundaramoorthi, Andrea Mennucci, Guillermo Sapiro, and Stefano Soatto.