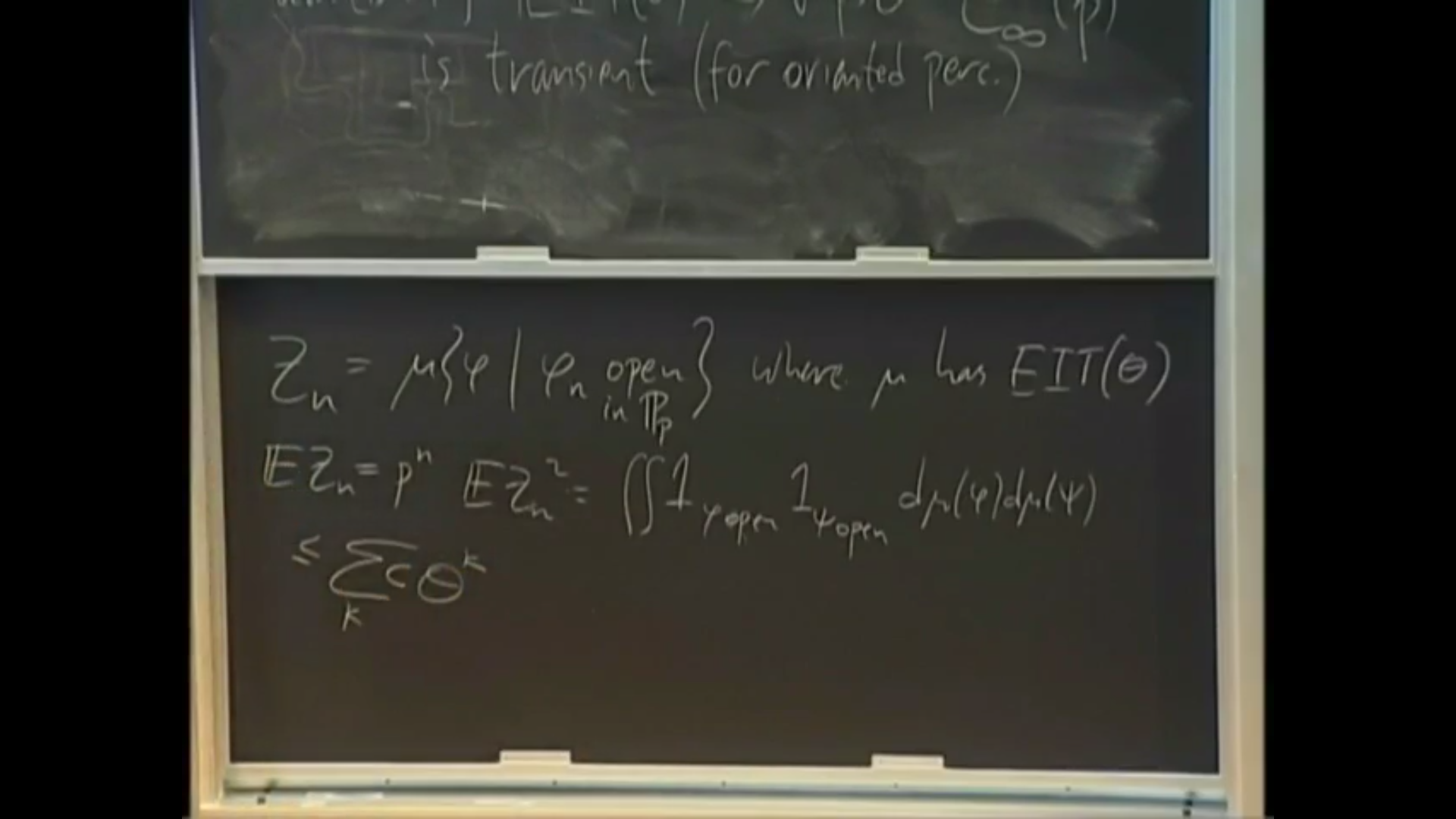Unpredictable paths and percolation
Presenter
February 22, 2012
Keywords:
- mathematical statistical mechanics
- probability theory
- percolation
- phase transitions
- scaling laws
- SLE
- Ising model
- unpredictable paths
- simple random walk
MSC:
- 82C20
- 82C26
- 82C27
- 82C05
- 82C44
- 82C43
- 82Cxx
- 82-xx
- 82C41
Abstract
Unpredictable paths in Z were introduced by Benjamini, Pemantle and the speaker in 1998, and used to prove transience of oriented percolation clusters in dimensions 3 and higher. An unpredictable path is a random nearest-neighbor path such that, given its past and present, the conditional probability it will be in a specified location k steps into the future decays faster than the decay rate for simple random walk (which is the reciprocal square root of k). Since then, several surprising applications were found, including a very recent application (with P. Sousi and P. Winkler) to a cop and Robber game. In this talk I will survey the applications as well as the sharp constructions and bounds by Haggstrom, Mossel, Hoffman and Sly.