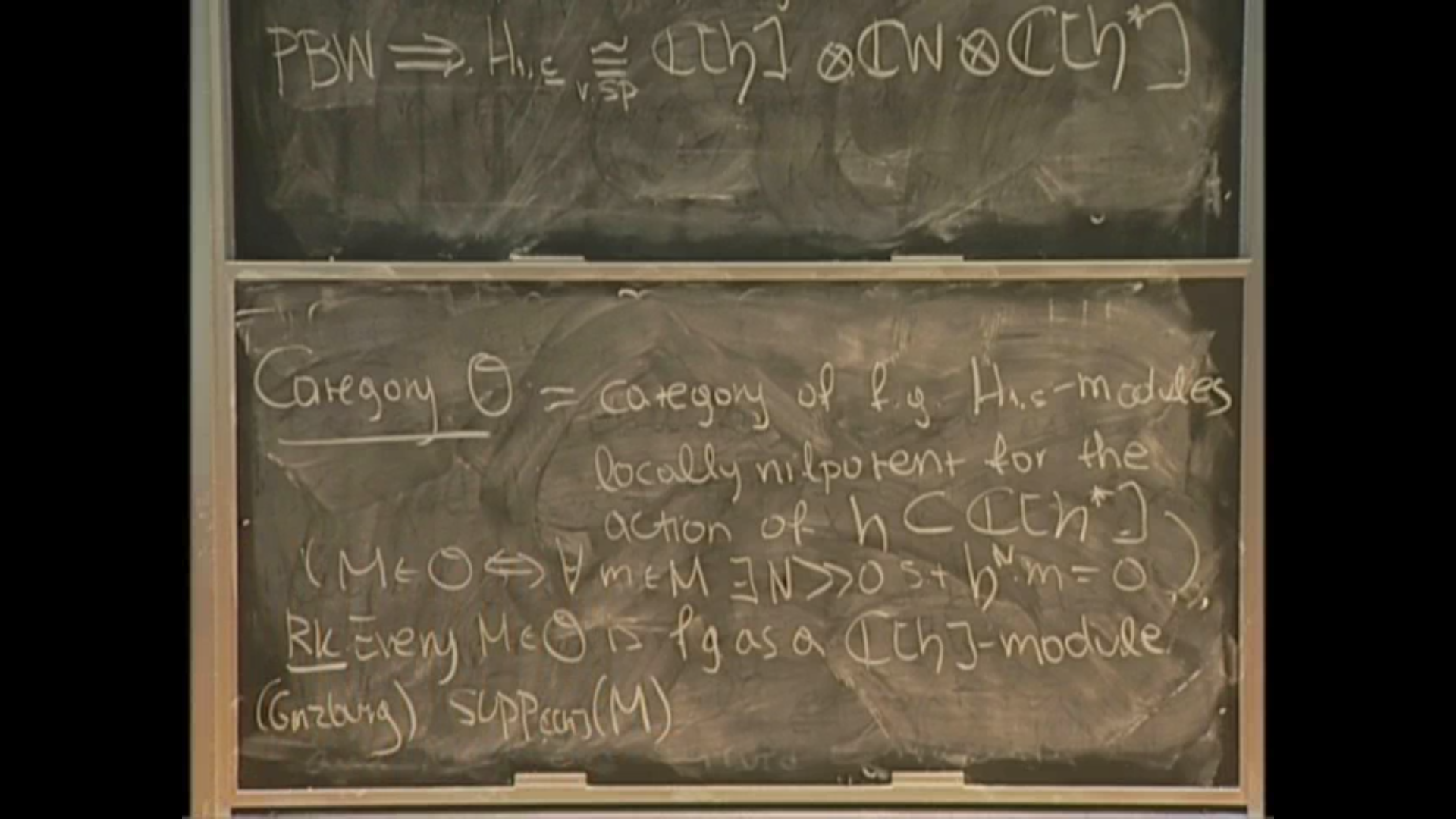Symplectic reflection algebras II
Presenter
February 1, 2013
Keywords:
- noncommutative algebraic geometry
- derived categories
- deformation quantization
- D-modules
- resolution of singularities
- rational Cherednik algebras
- Euler element
- Hecke algebra
- canonical bases
MSC:
- 13D09
- 13D10
- 13Dxx
- 13-xx
- 14Fxx
- 14F05
- 14F10
- 14A22
- 20C08
- 20Cxx
Abstract
Symplectic reflection algebras are related to a large number of areas of mathematics, such as combinatorics, integrable systems, D-modules, algebraic geometry, quiver varieties, symplectic resolutions of singularities and representation theory. In these lectures we will try to present some basic notions and results on this vast topic; we will see how the study of symplectic reflection algebras allows us to determine the existence of symplectic resolutions. We will then focus on a particular class of symplectic reflection algebras, the rational Cherednik algebras; we will explore their representation theory and its connections with the representation theory of Hecke algebras.