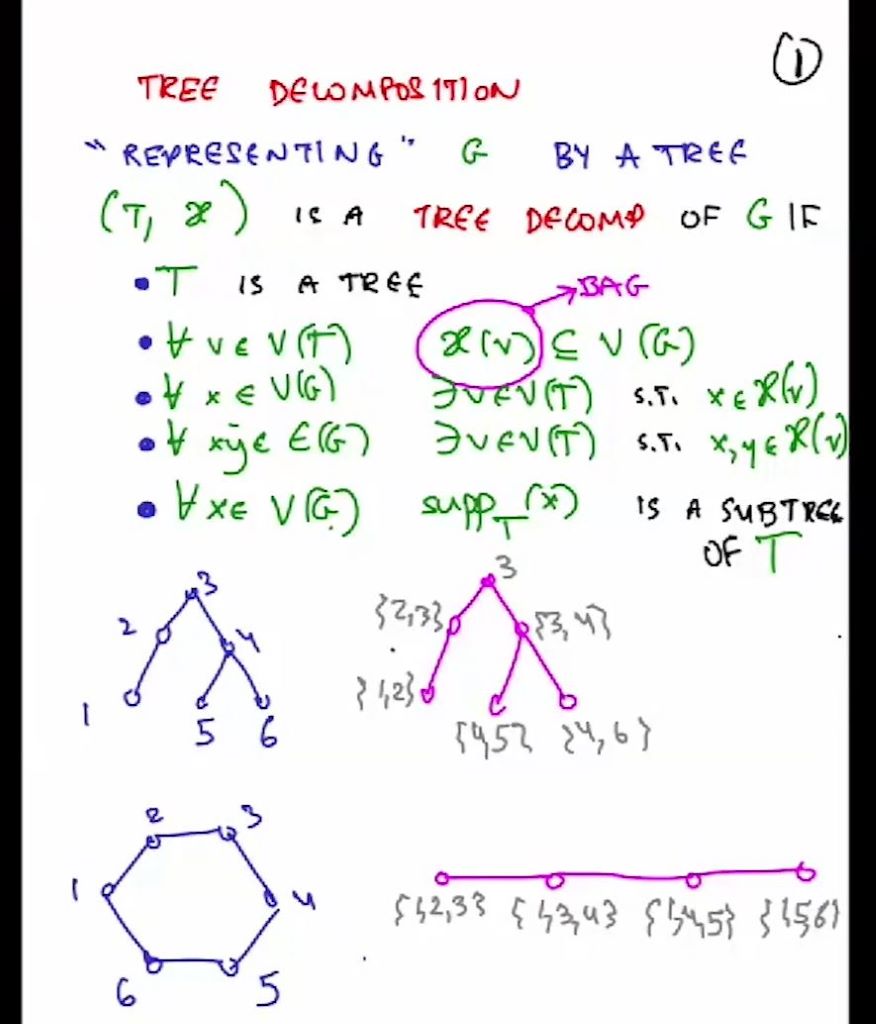
Tree decompositions are a powerful tool in both structural graph theory and graph algorithms. Many hard problems become tractable if the input graph is known to have a tree decomposition of bounded “width”. Exhibiting a particular kind of a tree decomposition is also a useful way to describe the structure of a graph. Tree decompositions have traditionally been used in the context of forbidden graph minors; studying them in connection with graph containment relations of more local flavor (such as induced subgraph or induced minors) is a relatively new research direction. In this talk we will discuss recent progress in this area, touching on both the classical notion of bounded tree-width, and concepts of more structural flavor. In particular we will describe a recent result providing a complete list of induced subgraph obstructions to bounded pathwidth.