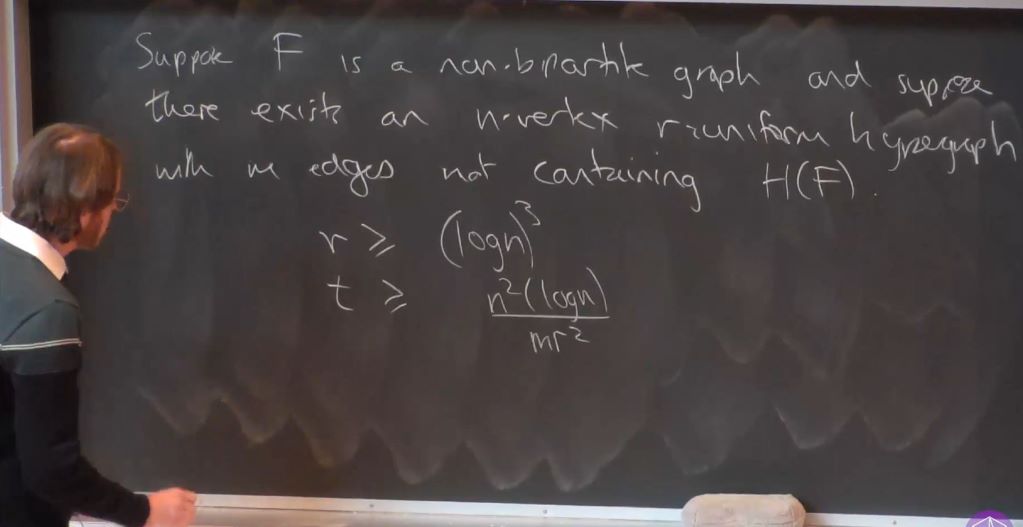Introductory Workshop - Graph Theory: Extremal, Probabilistic and Structural: Induced subgraphs of F-free graphs
Presenter
February 12, 2025
Keywords:
- extremal graph theory
- random graphs
- probabilistic methods
- structural graph theory
- Ramsey theory
MSC:
- 05C35 - Extremal problems in graph theory [See also 90C35]
- 05C55 - Generalized Ramsey theory [See also 05D10]
- 05C75 - Structural characterization of families of graphs
- 05C80 - Random graphs (graph-theoretic aspects) [See also 60B20]
- 05D40 - Probabilistic methods in extremal combinatorics
- including polynomial methods (combinatorial Nullstellensatz
- etc.)
Abstract
Given graphs F and G, the Erdos-Rogers function asks for the largest number of vertices in an F-free induced subgraph of every n-vertex G-free graph. These are generalizations of Ramsey numbers, and have been extensively researched in the literature. A key part of estimating these quantities is the same question in graphs of prescribed maximum degree. In this talk, we show that this quantity has two principal regimes, according as G is a subgraph of a blowup of F or not, and we use this result to give new bounds on Erdos-Rogers functions.
Joint work with D. Mubayi and P. Morawski