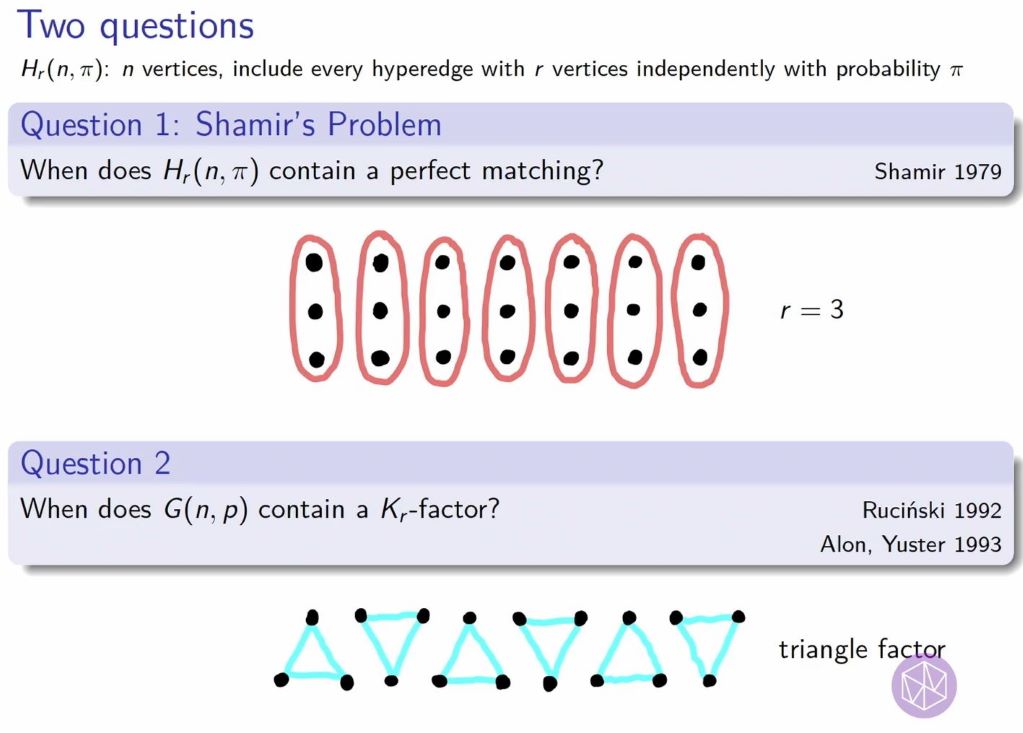
Let F be a graph on r vertices, and G a graph on n vertices. An F-factor in G is a subgraph of G consisting of n/r vertex-disjoint copies of F. When does G(n,p) contain an F-factor? In 2008, Johansson, Kahn and Vu found the (weak) threshold for 1-balanced F, along with the threshold for the closely related question of a perfect matching in the random r-uniform hypergraph (Shamir’s problem). In both cases, the main obstruction is the existence of isolated vertices — vertices not contained in any hyperedge (for Shamir’s problem) or not contained in any copy of F (for F-factors). Recently, Kahn solved Shamir’s problem completely, finding the sharp threshold and indeed proving a hitting time version in the random r-uniform hypergraph process. In this talk we discuss coupling arguments which allow us to find a copy of the random r-uniform hypergraph within the (vertex sets of) copies of F in G(n,p). This shows that the bulk of copies of F appear `morally independently’ in G(n,p). The starting point is a coupling due to Riordan when F is a complete graph on at least 4 vertices, or has certain `nice’ properties. We extend the result to all 1-balanced F, and also establish a process version for complete graphs F. Using these couplings and Kahn's result, we obtain the sharp threshold for the existence of an F-factor for all 1-balanced F. We also obtain the hitting time version when F is complete, showing that whp a K_r-factor exists in the random graph process as soon as every vertex is contained in a copy of K_r. Joint work with Fabian Burghart, Marc Kaufmann, Noela Müller, Matija Pasch.