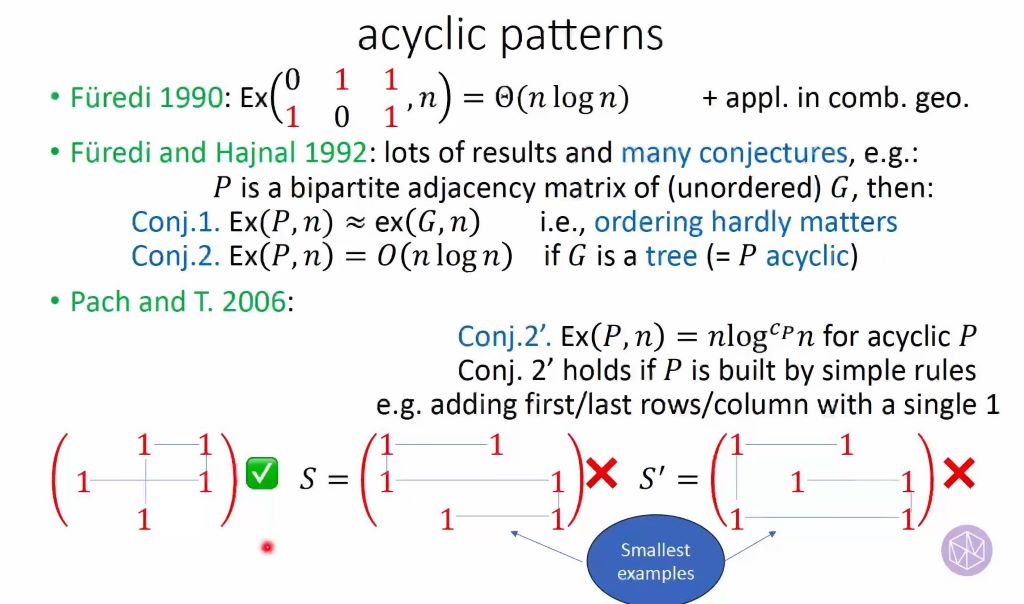
A zero-one matrix M is said to contain another zero-one matrix A if we can delete some rows and columns of M and replace some 1-entries with 0-entries such that the resulting matrix is A. The extremal function of A, denoted ex(n, A), is the maximum number of 1-entries that an n×n zero-one matrix can have without containing A. The systematic study of this function for various patterns A goes back to the work of Füredi and Hajnal from 1992. The field has many connections to other areas such as classical Turán type extremal graph theory and Davenport-Schinzel theory and has many applications in mathematics and theoretical computer science. The problem has been particularly extensively studied for so-called acyclic matrices and this talk is a survey of these results. After several refuted conjectures the one still standing (and wide open) states that the extremal function of any acyclic pattern is $n^{1+o(1)}$.