Modeling Molecular Kinetics with Koopman Operators and Kernel-based Learning
Presenter
May 13, 2024
Event: 41745
Abstract
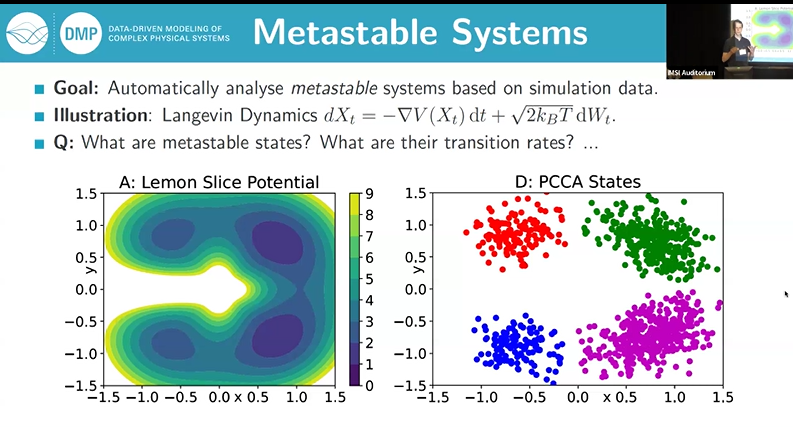
Koopman operator theory (Mezić, Nonlinear Dynamics, 2005) has emerged as a powerful modeling approach for complex dynamical systems arising in physics, chemistry, materials science, and engineering. The basic idea is to leverage existing simulation data to learn a linear model that allows to predict expectation values of observable functions at future times. Though the algorithm is conceptually quite simple, its underlying mathematical structure (the Koopman operator semigroup) is very rich, and can be used for different purposes including control, coarse graining, or the identification of metastable states in complex molecules and materials (Noé and Clementi, Current opinion in structural biology, 2017), (Klus, Nüske, Peitz et al, Physica D, 2020).
A critical modeling decision in this context is the choice of a finite-dimensional basis set (called dictionary). Kernel methods, which are well-known in other application areas of machine learning, have recently been shown to provide a powerful model class for Koopman learning, requiring only little prior information. The price to pay is that the dictionary size scales with the data size, leading to large-scale linear algebra problems that can become challenging to solve in practice. In this contribution (Nüske and Klus, Journal of Chemical Physics, 2023), we demonstrate that stochastic low-rank approximations based on Random Fourier features lead to reduced linear algebra problems that can be solved at much lower cost. We also show that hyper-parameters of the kernel can be tuned efficiently based on physical principles, allowing for an effective identification of metastable states in molecular systems.