Understanding diffusion in complex materials using machine learning and a variational approach
Presenter
May 16, 2024
Event: 41745
Abstract
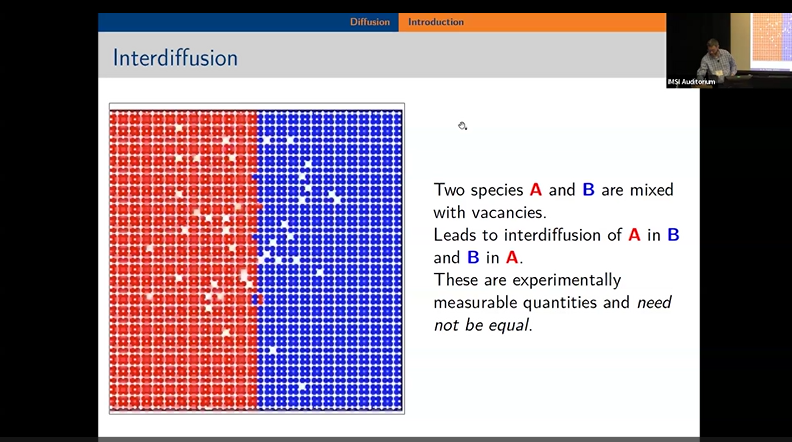
Computing diffusivity in solid systems from atomistic information can range from a very simple problem to an incredibly complex one. When written as the long-time limit of the mean-squared displacement, it requires long trajectories to converge to the true value, which can make direct simulation using kinetic Monte Carlo unattractive in some cases. This is especially true for complex materials with a variety of environments and transition rates, which can exhibit trapping and non-Arrhenius behavior of the diffusivity. An alternative to trajectories involves expressing the diffusivity with a variational principle, and numerically find the minimum. In addition, when we work with the variational form, new insights emerge. Using machine learning with a variational formula for diffusivity, we recast diffusion as a sum of individual contributions to diffusion---called ``kinosons''---and compute their statistical distribution. We apply this to model a complex multicomponent alloy. Calculating kinosons is orders of magnitude more efficient than computing whole trajectories, and elucidates kinetic mechanisms for diffusion. In particular, we see sluggish diffusion for the fastest species change with temperature. The density of kinosons with temperature leads to new accurate analytic models for macroscale diffusivity. This combination of machine learning with diffusion theory promises insight into other complex materials, making it useful for a wide variety of new problems in mass transport.