Videos

Recent progress on geometric analysis and Riemannian geometry: Uniqueness of Semigraphical Translators

Presenter
October 22, 2024
SLMath
Keywords:
  • mean curvature flow
  • Ricci flow
  • fully nonlinear flows
  • general relativity
  • mass
  • Ricci curvature
  • scalar curvature
  • sectional curvature
  • symmetry
  • Riemannian geometry
  • groups actions
  • minimal surfaces
  • stability
MSC:
  • 35-XX - Partial differential equations
  • 49-XX - Calculus of variations and optimal control
  • optimization
  • 53-XX - Differential geometry
  • 58-XX - Global analysis
  • analysis on manifolds
  • 83-XX - Relativity and gravitational theory
Play Video
Abstract
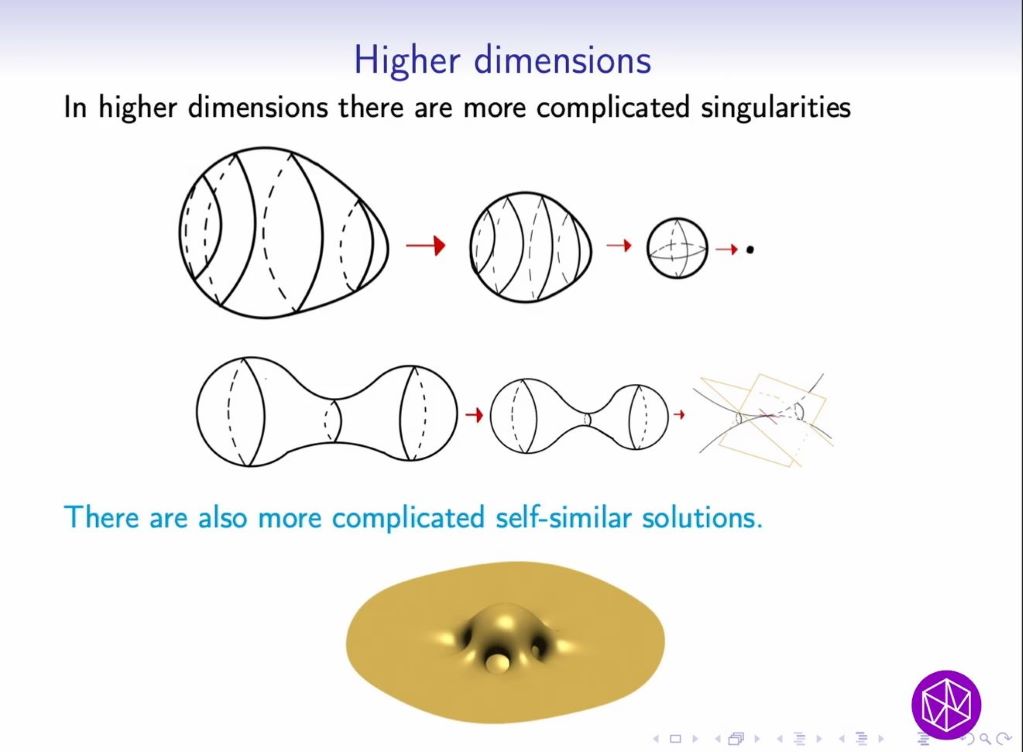
In this talk we prove the uniqueness of pitchfork and helicoid translators of the mean curvature flow in $\mathbb{R}^3$. This solves a conjecture by Hoffman, White and Martin. The proof is based on an arc-counting argument motivated by Morse-Rad\'o theory for translators and a rotational maximum principle. This is joint work with F. Martin and R. Tsiamis.