Introductory Workshop: Special Geometric Structures and Analysis: Structure of singularities for semicalibrated currents
Presenter
September 6, 2024
Keywords:
- Kähler manifolds
- Kahler metrics
- Einstein metrics
- canonical metrics
- special holonomy
- Calabi-Yau
- geometric elliptic and parabolic PDEs
- Pluripotential Theory
- variational approach
- Monge-Ampère equation
- area minimizing currents
- semicalibrated currents
- minimal surfaces
MSC:
- 32Q15 - Kähler manifolds
- 32Q20 - Kähler-Einstein manifolds
- 32Q25 - Calabi-Yau theory (complex-analytic aspects)
- 32Q57 - Classification theorems for complex manifolds
- 32U05 - Plurisubharmonic functions and generalizations
- 32W20 - Complex Monge-Ampère operators
- 35B65 - Smoothness and regularity of solutions to PDEs
- 35J47 - Second-order elliptic systems
- 49Q05 - Minimal surfaces and optimization
- 49Q15 - Geometric measure and integration theory
- integral and normal currents in optimization
- 49Q20 - Variational problems in a geometric measure-theoretic setting
- 53A10 - Minimal surfaces in differential geometry
- surfaces with prescribed mean curvature
- 53C07 - Special connections and metrics on vector bundles (Hermite-Einstein
- Yang-Mills)
- 53C38 - Calibrations and calibrated geometries
- 53C55 - Global differential geometry of Hermitian and Kählerian manifolds
Abstract
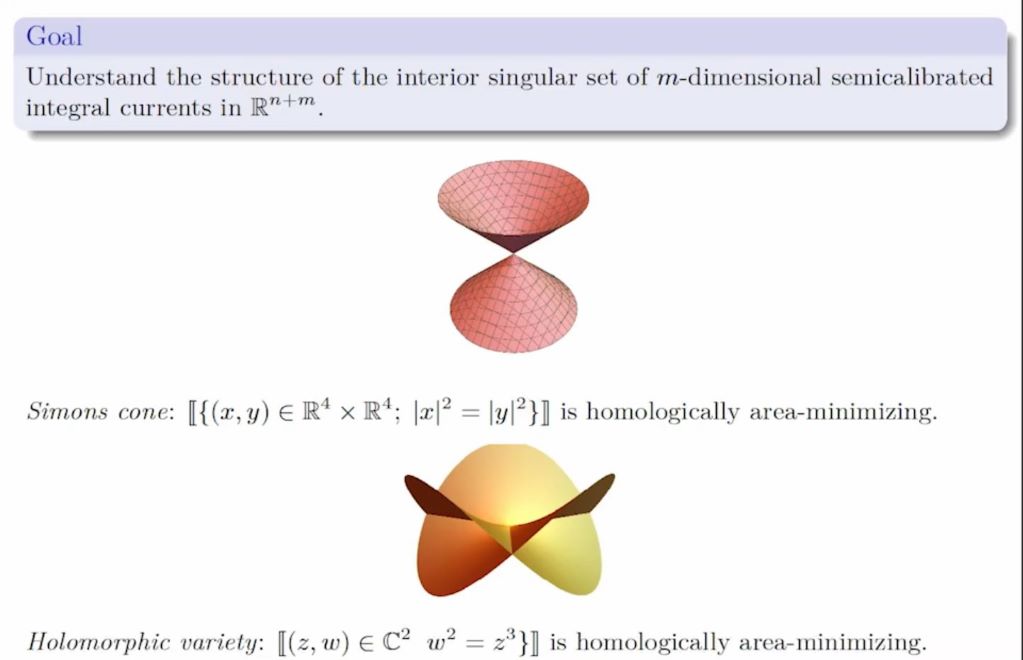
Semicalibrated currents are a generalization of calibrated submanifolds and appear naturally in various geometric problems, since the property of being merely semicalibrated is significantly easier to preserve under deformations. Semicalibrated currents are expected to share the regularity properties of area-minimizing currents, and indeed Almgren's celebrated dimension estimate on the interior singular set was shown to also hold for semicalibrated surfaces by Spolaor in 2015. I will talk about joint work with Paul Minter, Anna Skorobogatova, and Luca Spolaor, in which we build on this to establish a sharp structural result (rectifiability) for the interior singular set.