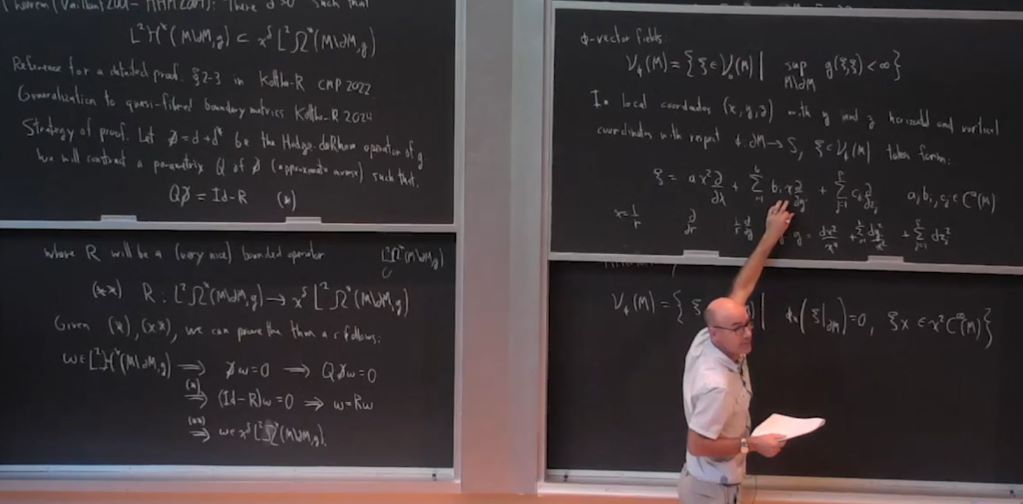Introductory Workshop: Special Geometric Structures and Analysis: Decay of L^2-harmonic forms via microlocal methods
Presenter
September 5, 2024
Keywords:
- Kähler manifolds
- Kahler metrics
- Einstein metrics
- canonical metrics
- special holonomy
- Calabi-Yau
- geometric elliptic and parabolic PDEs
- Pluripotential Theory
- variational approach
- Monge-Ampère equation
- area minimizing currents
- semicalibrated currents
- minimal surfaces
MSC:
- 32Q15 - Kähler manifolds
- 32Q20 - Kähler-Einstein manifolds
- 32Q25 - Calabi-Yau theory (complex-analytic aspects)
- 32Q57 - Classification theorems for complex manifolds
- 32U05 - Plurisubharmonic functions and generalizations
- 32W20 - Complex Monge-Ampère operators
- 35B65 - Smoothness and regularity of solutions to PDEs
- 35J47 - Second-order elliptic systems
- 49Q05 - Minimal surfaces and optimization
- 49Q15 - Geometric measure and integration theory
- integral and normal currents in optimization
- 49Q20 - Variational problems in a geometric measure-theoretic setting
- 53A10 - Minimal surfaces in differential geometry
- surfaces with prescribed mean curvature
- 53C07 - Special connections and metrics on vector bundles (Hermite-Einstein
- Yang-Mills)
- 53C38 - Calibrations and calibrated geometries
- 53C55 - Global differential geometry of Hermitian and Kählerian manifolds
Abstract
I will explain a general and flexible method originally introduced by Richard Melrose for estimating the decay of L^2-harmonic forms at infinity, but focusing on the specific example of L^2-harmonic forms of fibered boundary metrics (e.g. most types of gravitational instantons), in which case the result is due to Hausel-Hunsicker-Mazzeo in 2004 and heavily relies on the parametrix construction of Vaillant. After outlining the method, I will introduce the pseudodifferential calculus needed and describe the important steps of the parametrix construction. I will also indicate other important results that can be obtained with this method.