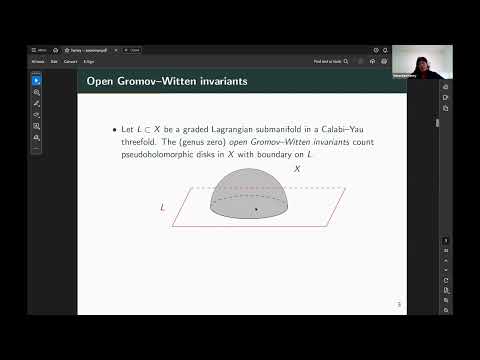
One of the earliest achievements of mirror symmetry was the prediction of genus zero Gromov-Witten invariants for the quintic threefold in terms of period integrals on the mirror. Analogous predictions for open Gromov-Witten invariants in closed Calabi-Yau threefolds can be formulated in terms of relative period integrals on the mirror, which govern extensions of variations of Hodge structure. I will discuss work in which I construct an immersed Lagrangian in the quintic which supports a family of objects in the Fukaya category mirror to vector bundles on lines in the mirror quintic, and deduce its open Gromov-Witten invariants from homological mirror symmetry. The domain of this Lagrangian immersion is a closed 3-manifold obtained by gluing together two copies of a cusped hyperbolic 3-manifold. The open Gromov-Witten invariants of the Lagrangian are irrational numbers valued in the invariant trace field of the hyperbolic pieces