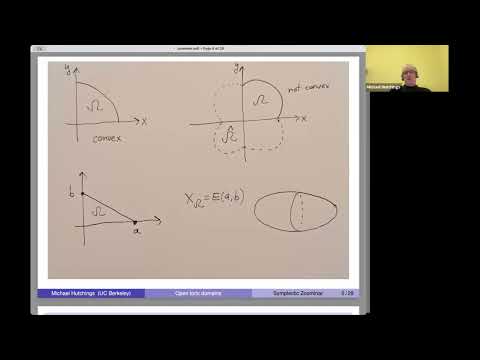
We show that two generic, open, convex or concave toric domains in R4 are symplectomorphic if and only if they agree up to reflection. The proof uses barcodes in positive S1-equivariant symplectic homology, or equivalently in cylindrical contact homology.