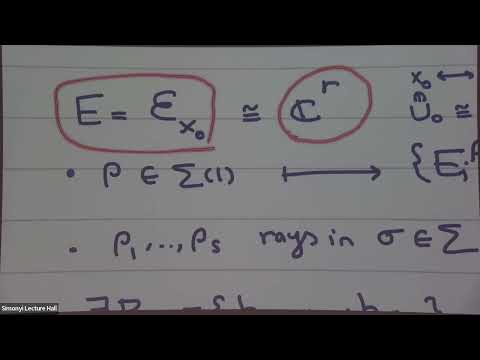A toric vector bundle is a torus equivariant vector bundle on a toric variety.We begin by recalling the classification of toric vector bundles due to Klyachko. The Klyachko data of a toric vector bundle can be interpreted as a "piecewise linear map" from the fan of toric variety to the space of valuations on a vector space. Motivated by this, we define the notion of a "piecewise linear map" from a fan to the Bergman fan of a matroid. We call this combinatorial object a "tropical toric vector bundle" (alternatively it can be called a "toric matroid bundle"). We define equivariant K-theory and characteristic classes of these bundles. As a particular case, we see that any matroid comes with tautological tropical toric vector bundles over the permutahedral toric variety and the corresponding equivariant K-classes and Chern classes recover the tautological classes of matroids constructed in the recent work of Berget-Eur-Spink-Tseng. In analogy with toric vector bundles, one can define sheaf of sections and Euler characteristic as well as positivity notions such as global generation, ampleness and nefness for tropical toric vector bundles and prove a kind of vanishing of higher cohomologies result. This is a joint work with Christopher Manon. We note that, independently and around the same time but from a different point of view, Khan and Maclagan also have arrived at (basically) the same notion (of a tropical toric vector bundle).